| Home Register Puzzles Solve Teams Statistics Rules Solving Guide F.A.Q. Archive mezzacotta |
Solution: 5C. Lines
We are presented with some possibly cryptic looking diagrams featuring coloured lines, and a page of numbers punctuated by slashes and commas. The first step is to recognise what the pictures represent.
Some experience with modern urban living in a big city will help, because the images are diagrams of train systems from various cities around the world, though stripped of helpful niceties such as station locations and names. An initial breakthrough might be made by recognising the metro systems of London or Paris, or a city you have visited, or simply by recognising the distinctive graphic features of modern metro maps. The puzzle title, "Lines", might also help to confirm this, if interpreted as "train lines".
Some of the maps can be identified with a bit of online research, but others may take considerable effort and only be resolved by the next working step. The maps are, in the order presented in the puzzle:
| Map | Metro | Map | Metro |
|---|---|---|---|
 | Paris Métro |  | Toronto Subway |
 | London Underground (the standard Tube map includes Docklands Light Rail, London Overground, and Croydon Tramlink) |
 | Brisbane (Queensland Rail City network) |
 | Washington D.C. Metro |  | Atlanta (MARTA) |
 | Sydney Trains |  | Brussels Metro |
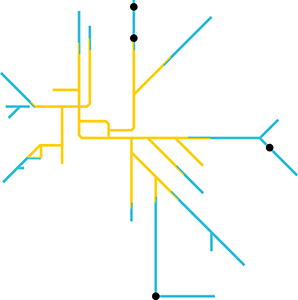 | Melbourne rail network |  | Montreal Metro |
 | Boston T |  | San Francisco (BART) |
The only features marked on each map besides the coloured train lines themselves are large black dots in various locations. These are the locations of specific stations. Referring to current metro maps of each city reveals the stations to be:
| City | Stations |
|---|---|
| Paris | Bourse, Chaussée d'Antin – La Fayette, Saint-Michel, Saint-Paul |
| Toronto | Museum, Union |
| London | Bayswater, Richmond, St Paul's, Stanmore |
| Brisbane | Fairfield, Milton |
| Washington D.C. | Clarendon, Union Station |
| Atlanta | Airport, Ashby |
| Sydney | Clarendon, Epping, Fairfield, Macarthur, Museum, Stanmore |
| Brussels | Bourse, Parc |
| Melbourne | Bayswater, Epping, Frankston, Reservoir |
| Montreal | Parc, Saint-Michel |
| Boston | Airport, Milton, Reservoir |
| San Francisco | Ashby, Lafayette, MacArthur, Richmond |
It is not too difficult to notice that many of the station names are repeated in different cities. In fact, taking some small liberties in matching up "Chaussée d'Antin – La Fayette" to "Lafayette", "Saint-Paul" to "St Paul's", and so on, we see that every station matches exactly one other station, with the leftover singleton of Frankston. This indicates there is something special about Frankston.
Noticing that the stations names occur in pairs is also a way to fill in any of the missing metros that might be difficult to identify otherwise. For example, if Brussels is missing (possibly the hardest one to identify), one might surmise that the two marked stations must be from the set {Bourse, Frankston, Parc}. A bit of trial and error with an Internet search engine, perhaps speculating that the result should be in a Francophone country, should lead to the identification. Similar deductions can be made if other cities are missing.
A little more thinking on the complete list of stations might also reveal another possible anomaly. All the cities have an even number of stations listed, except Boston, which has three. With or without this realisation, we can start on the next step of the solution.
The intuitive leap to make is that we can form a sort of "journey" across all of these cities, starting at one point, and then "transferring" to another train in a new city at a station which shares a name between cities. Given Frankston is the odd place out, it makes sense to see if we can begin here. The options are to travel from Frankston to either:
- Bayswater, and then transfer to Bayswater in London.
- Epping, and then transfer to Epping in Sydney.
- Reservoir, and then transfer to Reservoir in Boston.
Once we've made a decision, the possible routes branch even more. One method to attack this problem is to notice that some cities only have two stations, so the route through them is clear. Using these we can form some unambiguous chains:
- Bourse (Paris) - Bourse (Brussels) - Parc (Brussels) - Parc (Montreal) - Saint-Michel (Montreal) - Saint-Michel (Paris).
- Museum (Sydney) - Museum (Toronto) - Union (Toronto) - Union Station (Washington) - Clarendon (Washington) - Clarendon (Sydney).
- Ashby (San Francisco) - Ashby (Atlanta) - Airport (Atlanta) - Airport (Boston).
- Fairfield (Sydney) - Fairfield (Brisbane) - Milton (Brisbane) - Milton (Boston).
If we think about the possible routes we can form a few possible complete journeys. This, or perhaps some graph theory similar to the Seven Bridges of Königsberg problem, may reveal that the end of our journey must lie in Boston. To disambiguate and decide on the final route, we need to turn to the other information supplied in the puzzle: the list of numbers.
The numbers are presented in 19 separate rows. Each row contains a comma-separated list of pairs of numbers separated by slashes. The first number in each pair increases monotonically, going as high as 44, while the second number seems more random, but biased towards lower numbers. A count of our proposed train journey reveals there will be 18 legs, which almost matches the number of rows of numbers. One might speculate that each row represents one train leg, with the mystery of the final row to be revealed later.
Looking for ways to extract a message, a reasonable intuitive leap is that the first number in each pair (uniformly increasing) might refer to stations, numbered as we pass them, while the second number could be used to extract a letter from the indicated station's name. Trying this on the trip from Frankston north towards the three other Melbourne stations produces the promising looking WHATDIDT if we take the route to Bayswater; whereas if we go to Reservoir we run out of stations, and if we go to Epping we get WHATOUKO.
Selecting Bayswater and continuing our journey in London, we can eventually piece together a coherent route and what looks like a message:
| City | Station | Station number | Letter number | Letter |
|---|---|---|---|---|
| Melbourne | Frankston | 0 | - | |
| Hawksburn | 23 | 2 | W | |
| Richmond | 25 | 4 | H | |
| East Richmond | 26 | 2 | A | |
| Hawthorn | 28 | 4 | T | |
| Nunawading | 40 | 7 | D | |
| Mitcham | 41 | 2 | I | |
| Heatherdale | 42 | 8 | D | |
| Heathmont | 44 | 4 | T | |
| Bayswater | - | - | ||
| London | Bayswater | - | - | |
| Notting Hill Gate | 1 | 8 | H | |
| Queensway | 2 | 3 | E | |
| Bond Street | 5 | 4 | D | |
| Oxford Circus | 6 | 1 | O | |
| Holborn | 8 | 3 | L | |
| Chancery Lane | 9 | 9 | L | |
| St Paul's | - | - | ||
| Paris | Saint-Paul | - | - | |
| Rambuteau | 2 | 3 | M | |
| Arts et Métiers | 3 | 1 | A | |
| Bourse | - | - | ||
| Brussels | Bourse | - | - | |
| De Brouckere | 1 | 8 | K | |
| Gare Centrale | 2 | 4 | E | |
| Parc | - | - | ||
| Montreal | Parc | - | - | |
| Fabre | 3 | 4 | R | |
| Saint-Michel | - | - | ||
| Paris | Saint-Michel | - | - | |
| Palais Royal – Musée du Louvre | 4 | 21 | U | |
| Pyramides | 5 | 9 | S | |
| Opéra | 6 | 3 | E | |
| Chaussée d'Antin – La Fayette | - | - | ||
| San Francisco | Lafayette | 0 | 7 | T |
| Orinda | 1 | 1 | O | |
| MacArthur | - | - | ||
| Sydney | Macarthur | - | - | |
| Campbelltown | 1 | 1 | C | |
| Leumeah | 2 | 6 | A | |
| Ingleburn | 4 | 7 | U | |
| Casula | 7 | 3 | S | |
| Liverpool | 8 | 4 | E | |
| Fairfield | - | - | ||
| Brisbane | Fairfield | 0 | 3 | I |
| Dutton Park | 1 | 6 | N | |
| South Bank | 3 | 1 | S | |
| Roma Street | 5 | 4 | A | |
| Milton | - | - | ||
| Boston | Milton | - | - | |
| Ashmont | 3 | 6 | N | |
| Fields Corner | 5 | 2 | I | |
| South Station | 10 | 4 | T | |
| Boylston | 13 | 3 | Y | |
| Arlington | 14 | 1 | A | |
| Hynes | 16 | 3 | N | |
| Longwood | 19 | 8 | D | |
| Beaconsfield | 22 | 4 | C | |
| Reservoir | - | - | ||
| Melbourne | Reservoir | - | - | |
| Keon Park | 2 | 3 | O | |
| Lalor | 4 | 5 | R | |
| Epping | - | - | ||
| Sydney | Epping | - | - | |
| Rhodes | 5 | 1 | R | |
| Auburn | 10 | 2 | U | |
| Parramatta | 14 | 1 | P | |
| Toongabbie | 18 | 1 | T | |
| Vineyard | 25 | 2 | I | |
| Clarendon | - | - | ||
| Washington | Clarendon | - | - | |
| Foggy Bottom-GWU | 3 | 2 | O | |
| Metro Center | 6 | 8 | N | |
| Union Station | - | - | ||
| Toronto | Union | - | - | |
| Queen's Park | 4 | 8 | A | |
| Museum | - | - | ||
| Sydney | Museum | - | - | |
| Central | 1 | 4 | T | |
| Newton | 4 | 4 | T | |
| Stanmore | - | - | ||
| London | Stanmore | - | - | |
| Dollis Hill | 6 | 7 | H | |
| West Hampstead | 9 | 2 | E | |
| Willesden Junction | 13 | 5 | E | |
| Gunnersbury | 16 | 3 | N | |
| Kew Gardens | 17 | 7 | D | |
| Richmond | - | - | ||
| San Francisco | Richmond | - | - | |
| Downtown Berkeley | 4 | 2 | O | |
| Ashby | - | - | ||
| Atlanta | Ashby | - | - | |
| Five Points | 3 | 1 | F | |
| West End | 5 | 4 | T | |
| Lakewood/Fort Mcpherson | 7 | 16 | H | |
| College Park | 9 | 5 | E | |
| Airport | - | - | ||
| Boston | Airport | - | - |
In some cases, particularly with Paris and London, the intended route to take may not be entirely clear, as there are several options involving the interconnecting lines. These can be resolved by trial and error, using the indexing to see which route produces a sensible message. Probably the trickiest is the route from Saint-Michel to Chaussée d'Antin – La Fayette in Paris. There are shorter routes in terms of stations visited (such as Saint-Michel, Musée d'Orsay, Invalides, Concorde, Madeleine, Opéra, Chaussée d'Antin – La Fayette; taking 6 stops), but the intended route is the one that an actual traveller would be most likely to choose because it involves just one change of trains, rather than multiple changes (Saint-Michel, Cite, Chatelet, Pont Neuf, Palais Royal – Musée du Louvre, Pyramides, Opéra, Chaussée d'Antin – La Fayette; taking 7 stops).
The message spells out: WHAT DID THE DOLLMAKER USE TO CAUSE INSANITY AND CORRUPTION AT THE END OF THE. This does not seem like a complete sentence, and we still have the so far unused 19th line of numbers to use. The intuitive leap here is that the journey actually continues beyond Airport (Boston), to an unspecified end point. From Boston's Airport we can travel in two directions. Trying them, we find a sensible completion of the message by travelling north:
| City | Station | Station number | Letter number | Letter |
|---|---|---|---|---|
| Boston | Airport | - | - | |
| Wood Island | 1 | 7 | L | |
| Orient Heights | 2 | 3 | I | |
| Beachmont | 4 | 8 | N | |
| Wonderland | 6 | 5 | E |
The completed message is: WHAT DID THE DOLLMAKER USE TO CAUSE INSANITY AND CORRUPTION AT THE END OF THE LINE? The "end of the line", both in the sense that it is the final destination, and that it is literally the end of the blue line of the Boston T system, is Wonderland.
Combining these clues, it's possible to determine that these are referencing the computer game Alice: Madness Returns. Based on the Alice in Wonderland stories of Lewis Carroll, the plot of the game involves a villain named The Dollmaker who corrupts Wonderland, causing insanity in Alice and other denizens. The tool he uses to cause all of this is the Infernal Train, a madness-inducing locomotive.
This provides a connection back to trains, the theme of the puzzle. The solution is THE INFERNAL TRAIN, or INFERNAL TRAIN (both answers accepted).
Puzzle designer's notes
I had the idea for this puzzle while visiting San Francisco, and travelling on its BART train system. Looking at the system map, I noticed it had stations named MacArthur and Richmond, both of which are also the names of stations in my home city of Sydney. I idly daydreamed what it would be like if I could catch a train in San Francisco and travel to Sydney, via one of these stations, instead of having to endure a 14-hour flight.
Back at home, I checked a few other metro systems which I've ridden over many years of travel, including London and Boston, and found a few other such coincidences. This seemed like the kernel of a puzzle, so I began more extensive research. A virtual trip around the world, changing trains at similarly named stations in various metro systems, seemed pretty cool.
To find the connections, I scanned the metro maps for places like Boston and San Francisco, searching for stations with the same names but in other cities. It wasn't too hard finding a cluster based on Australian cities and London, since many Australian suburbs are named after or in the style of British places. The American cities were a bit trickier, as I'm less familiar with those. And I wanted to include Paris, but it was tricky finding place names that existed both in English and French speaking cities. Besides St Paul's, Paris and London also share a Temple station; and besides Lafayette, Paris and San Francisco have Concorde/Concord.
To get more use out of Paris, I checked some other Francophone cities, finding matches in Montreal and Brussels, so they went into my tentative list. I also found a very interesting possibility in the Dubai Metro, which contains both a station named Union (matching Toronto and Washington), and a station named Danube (matching one in Paris). I woud have liked to get some more exotic cities included, especially Rome, but alas Rome's stations all have extremely Italian names which simply don't exist outside Italy. After building up a list which looked suitably large, I drew a graph of all the possible connections:

Now to find an interesting route which used as many of the connections as possible! This was very much a Seven Bridges of Königsberg problem, as I realised all cities except the beginning and end would have to have an even number of stations used. Inevitably, this meant some of the connections had to be discarded. Furthermore, at this point I settled on the theme of the puzzle. Ever since my first visit to Boston, I'd been intrigued by the name of the station Wonderland, lurking there at the top of the Boston T map. I have since discovered it was named indirectly after an amusement park, via a greyhound racing track. Testing "wonderland" and "train" in a search engine, I stumbled across the Infernal Train in Alice: Madness Returns, and knew what the final answer of the puzzle had to be.
Eventually I settled on the route used in the puzzle, ending at Wonderland, and then set about creating the hidden message. In the first draft of the puzzle, the route ended at Airport in Boston, and the message said "what caused the madness and corruption which await to the north". The test solvers successfully extracted the message, but then had no idea what to do with it, not connecting "to the north" with the station Wonderland further north of Airport. So the message was refined to be more explicit, and the route extended so that it actually ended at Wonderland, cluing it directly in the message with the "end of the line" reference.
On a second test solve, the feedback came through that the routes through Paris were difficult (though not impossible) to figure out, in particular the multiple choices for Saint-Michel to Chaussée d'Antin – La Fayette. Since my preferred route passed through the station with the impressively long name of "Palais Royal – Musée du Louvre", it was suggested to use a really high number to index the U in Louvre, thus making it clear that none of the other likely routes held a station with a long enough name.
In each case, the puzzle uses the most recent available official map of the respective train systems. Many of these maps have been modified many times over the years, adding new lines or adjusting the geometry, and searching online sometimes brings up historical versions, so some effort was taken to find the current versions to give a specific and sensible baseline.
Each map was traced in Inkscape to produce a vector illustration facsimile of the maps showing only the lines, and the black dots were centred as exactly as possible on the relevant stations, so they could be identified unambiguously if teams overlaid the puzzle on a current metro map with transparency. (Although the fact that every station but Frankston is repeated in name should disambiguate if it's not clear which station any given black dot is closer to.)
I hope train fans had as much fun with this puzzle as I had creating it.
