Home     Register     Puzzles     Solve     Teams     Statistics     Rules     Solving Guide     F.A.Q.     Archive     mezzacotta

Solution: 1E. Five Squares Plus Another Five Squares

We start by solving the clues. From the provided grids, the answers are expected to be five letters long. After finding some of the obvious answers, it becomes apparent that the clues have been arranged so that the answers are in alphabetical order. This helps narrow down options and resolve ambiguities.

Taking the alphabetical ordering into account, most answers should be easy to determine. A few answers may require a bit of searching or a handy grounding in trivia:

• The seed fibre is akund.
• The Hungarian revolution is the Aster Revolution.
• The ear bone is the incus; 'anvil' also has five letters, but does not fit alphabetically.
• 'Orris' can refer to either certain irises or gold or silver lace.
• The World of Warcraft seer is named Takar.
• The youngest daughter of Karl Marx was Jenny Julia Eleanor Marx, who was nicknamed 'Tussy'.
• The clue about the radio star is a reference to the song Video Killed the Radio Star by The Buggles.

The full list of the intended answers is:

Correctly placing the words gives us the two grids below (there is an explanation of the placement process at the end of this solution). In each grid we could swap across with down, and we could also swap SHARK with SLICK; neither matters as far as the rest of the solution goes.

Now comes the time for an intuitive leap. After staring at the completed grids for a while, it may be noticed that some of the "adjacent" five-letter words can be turned into eleven-letter words by insertion of a single letter. For instance, ELECT and RATES can be joined with an O to make ELECTORATES. The puzzle title, originally taken to refer to the five large squares forming each grid, can also be considered to describe this step: each word is five squares, and joining it with another word (another five squares) gives something longer.

It turns out that this can be done for each of the central sets of five-letter words. Doing so then produces some two-letter fragments, and we again see that we can turn these into five-letter words by insertion of another extra letter. Doing so completely fills in the central cross-shaped portion of each grid. The puzzle title can be interpreted as describing this, too: To each grid we have added another five squares in the shape of a plus.

We end up with the following completed grids:

The (very!) uncommon word "Ushak" is a short form of "Ushak carpet". (see, for instance, Merriam-Webster's entry for "Oushak", which they list "Ushak" as a variant spelling of). A more common word would have been desirable, but any doubts about the correctness of this would be resolved by the next steps.

To each grid we have added five extra letters. We can anagram each to get two five-letter words: MOUTH and ASHES. We once more apply the step of making an eleven-letter word by insertion of an extra letter, giving us the final solution to the puzzle: MOUTHWASHES.

Author's notes

I had the idea for this puzzle in late 2012, after playing The Fool and his Money by Cliff Johnson. (If you are not familiar with his work then I strongly encourage you to play the original The Fool's Errand (available for free), and then buy and play The Fool and his Money.)

One of the puzzles in The Fool and His Money involved five-letter words, interlinked in a similar way to the grids of this puzzle. I recall thinking at the time that the negative space of the central cross cried out to be filled, and felt that he had missed a trick by not doing so.

This seemed like it had puzzle potential. The shape of what I wanted was already clear: twenty five-letter words, arranged into five large squares and interlocking in such a way that the central cross could be filled in to give four eleven-letter words and a further two five-letter words. For answer extraction purposes, I wanted the five extra letters to also form a word. The working title "Five Squares" was chosen at this point, superficially referring to the large squares but intended as a reference to the five "missing" squares of the central cross.

I generated a list of suitable eleven-letter words, but inspection showed that there were too many unusable options; I was paying the price for using an extensive word list with far too many obscure five-letter words in it. I spent the next day or so going through this list and weeding out uncommon entries, until I was left with a list of 279 candidates to generate grids from. I then put this list aside and forgot about it for three and a half years.

When it looked like there would be a 2016 competition (although no longer under the auspices of CiSRA), I remembered this puzzle idea and decided to see if it could be completed. It seemed likely that there was enough leeway for a grid to be constructed from common words, but it was rather less likely that a satisfying thematic answer might result.

I whipped up a program to find all grids using my list of candidate eleven-letter words and my system dictionary's list of five-letter words. (The grids were simplified by excluding the outer words, which would not affect the puzzle and could be filled in later with anything convenient.) Somewhat to my surprise, there were over a hundred thousand solutions! This was an embarrassment of riches — amongst so many, how might I find the desirable grids?

However, checking a few random solutions revealed problems: They were all unusably bad, in the sense that the five-letter words involved were mostly not what I would regard as words at all (whether because they were very obscure, or because they were proper nouns). And I certainly did not relish the prospect of looking through so many grids in search of something usable, if such even existed.

Looking for ways to simplify my search, I decided to extract all the used five-letter words from these solutions. There turned out to be a little under fifteen thousand of those, and it was just feasible to search through those and reject anything too unwordlike, or at least too difficult to clue. Many tedious hours later I had a list of almost four thousand usable five-letter words, and was able to embark on the next step.

Every solution so far used six five-letter words (plus another that would be formed from the extra letters, but I ignored that aspect for the time being). I scored each solution by how many of those appeared in the usable list, and was very happy when there were a small number of items that scored six.

Further difficulties presented themselves, however: Many of these solutions used the same five-letter word twice, whether on their own or as part of the eleven-letter words (e.g., 'interesting' and 'intertwines'). They were obviously unusable (and I should have filtered them out earlier, if it had occurred to me to check for that). In others, the resulting word formed by the extra letters was not usable. Of the 64 supposed candidates, only two passed muster.

The first of those was excellent as far as the five-letter words went, and would produce "pietà". However, I felt that the eleven-letter words were not as discoverable as I would like ("inter(e)sting" was excellent on that front, but the others were "hands(p)rings", "mills(t)reams", and "polar(i)sable"). The other (which would produce "bimbo") had some nice elevens, including my favourite of "titan(o)there", but had a fatal flaw: The connecting letters between the central and top left squares were the same. That meant that the top left square could be flipped about its major diagonal and still fit, and that could make it impossible to see the eleven-letter words.

So I dipped into some lower-scoring solutions, and found the grid that produced "mouth". I felt that the eleven-letter words for this were rather more discoverable, and further checking turned up nothing that seemed better. I wrote up some basic clues and sent it off for test solving.

I was not entirely happy with the result, though, since it felt like the answer lacked a good connection to the puzzle. The next day it finally dawned on me that I really should have been aiming for the recursive step of two five-letter words that would lead to another eleven. I had doubts about this being possible, but it was so clearly a more elegant option that I had to try. Fortunately I had saved all the solutions!

This time there were only a handful of potential pairs that might work. Three of the top four fell victim to issues that had ruled out single grids earlier (duplication of five-letter words and ambiguous connections), and everything lower had so few sensible five-letter words that they were unusable. That left only one candidate pair of grids, which were made into this puzzle. By happy fortune one of those was the same grid that had already produced "mouth", so I had not wasted that work.

The second grid had lovely eleven-letter words, which made me very happy, but one of the discovered five-letter words was "Ushak". Searching for this does turn up a Merriam-Webster definition as a variant spelling of "Oushak", a type of rug, but it's obviously not something that could be expected to be known. I tried to mangle the grid to produce an alternative, but the requirement for the word to match ?SHA? left only "pshaw" as a plausible replacement. That, in turn, would have required justifying "akpnd" as an answer. I spent a goodly while trying to make that fit, and even considered giving up and having a clue just be "Akpnd. No, really. Just go with it." Eventually I decided that "Ushak" was the lesser evil.

Another minor issue was that the outer words "shark" and "slick" could not be placed uniquely. I hoped that this would not be too discouraging to solvers; it is certainly a niggle that I would have preferred to avoid if possible, but the ambiguity was required by the rest of the grid.

A final concern was that the original puzzle title was no longer accurate. For a while the working title was "Five Squares, Times Two", but eventually I settled on the final title which can be considered to refer to at least three different aspects of the puzzle.

Overall, it was satisfying, and a little surprising, to actually end up with a usable puzzle based on the original idea. At the same time I can't help but wish that those rough edges could have been smoothed away; if only the English language had been a bit more cooperative!

Placing the words in the grids

We have the list of words:

Now we want to place the words into the provided grids. We can see that each grid consists of five interlocked squares of four words each; the puzzle title thus describes the pair of grids. Already we can see that there is some abiguity of placement due to the symmetry of the grids: In either completed grid we can swap across answers with down answers. Presumably this will not matter in the end, so we will choose an orientation when necessary and hope for the best.

The first step for placement is to find the individual squares; as mentioned, there is an across/down symmetry that we will worry about later. When forming squares, all we care about are the first and last letters in each answer. In a completed square, the top-left corner letter must start two words, the bottom-right corner letter must end two words, and the other two corner letters must each start one word and end another. If we think of letters as vertices in a graph, and each word as a directed edge from its first letter to its last letter, then each square corresponds to a part of the graph that looks like this:

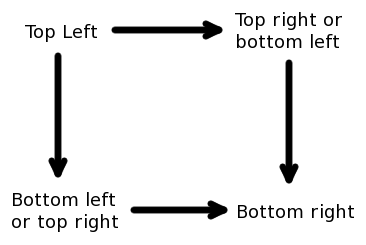
If we then make the full graph by using all words, we can find many of the squares by inspection. After removing the corresponding edges from the graph we can continue this process, and so identify all the squares (up to starting and ending letters, that is). Note that two vertices in a square could be the same letter, which would change the appearance of the corresponding part of the graph, but they are still easy to pick out.

The full graph of connections looks like this:

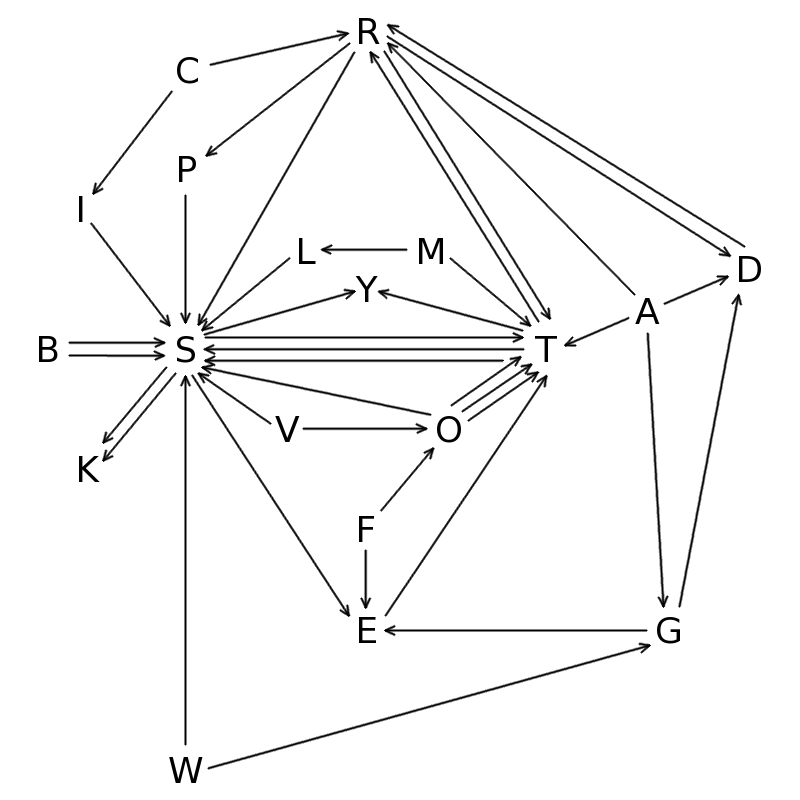
Some squares stand out immediately, and we can successively pull them out. There are still some uncertainties due to words like TACKS and TONES that have the same starting and ending letter, but later steps should sort that out.

• C points only to R and I, I only points to S, so we have a square from (CHILI, CHOIR, INCUS, RATES).
• B only points to S, twice, so it is the top left letter of its square and we need a letter that S points to twice. The only such is K, giving the square (BANKS, BOUTS, SHARK, SLICK).
• M points only to L and T, with L pointing only to S, giving us the square (MODEL, MOUNT, LEVIS, TACKS/TONES).
• V points only to O and S, with the other letter being T to form the square (VIRUS, VIDEO, SPORT, OCTET/OUGHT/OVERT).
• R points to P which points to S, and this can only be completed with a T, giving (RECAP, ROUST, PLAYS, TACKS/TONES).
• W points to S and G, and can only complete with E, giving (WRING, WANDS, GRAVE, SMOKE).
• F points to O and E, which can only complete with T to get (FORGE, FRODO, ELECT, OCTET/OUGHT/OVERT).
• The only remaining links with S are Y and O, with the other letter being T to give (ORRIS, OCTET/OUGHT/OVERT, SAPPY, TUSSY).
• The remaining links with G are A and D, completed with R to give (APING, ASTER, GOURD, RAPID).
• And the last remaining square is (AKUND, AVAST, DONOR, TAKAR).

Making arbitrary choices about across/down orientation, we have ended up with the following squares (with '.' used to represent uncertain letters):

CHILI   BANKS   MODEL   VIRUS   RECAP
H   N   O   .   O   E   I   P   O   L
O   C   U   .   U   V   D   O   U   A
I   U   T   .   N   I   E   R   S   Y
RATES   S...K   T...S   O...T   T...S

WRING   FORGE   ORRIS   APING   AKUND
A   R   R   L   .   A   S   O   V   O
N   A   O   E   .   P   T   U   A   N
D   V   D   C   .   P   E   R   S   O
SMOKE   O...T   TUSSY   RAPID   TAKAR

Now that we have the individual squares (mostly), we need to find the right way to link five of them together to fit inside a grid. For the linking, the relevant letters are those pairs adjacent to the corners (e.g., for CHILI / CHOIR / INCUS / RATES the pairs are HH, LN, AI, and EU). Two linked squares will have the same pair of letters next to one of their corners. (Note that due to the across/down symmetry we must treat these as pairs without order.)

So we tabulate the pairs for each of the squares we have found, and aim to find a square where all its pairs are also found in other squares. That square should then be a central square, and we can place the other squares around it. The sets of pairs that we get are:

(CHILI, CHOIR, INCUS, RATES)	HH	LN	AI	EU
(BANKS, BOUTS, SHARK, SLICK)	AO	HN/KL	HT/LT	CR
(MODEL, MOUNT, LEVIS, TACKS/TONES)	OO	EE	AN/NO	EI/IK
(VIRUS, VIDEO, SPORT, OCTET/OUGHT/OVERT)	II	PU	CE/EU/EV	ER/HR/RR
(RECAP, ROUST, PLAYS, TACKS/TONES)	EO	AL	AS/OS	EY/KY
(WRING, WANDS, GRAVE, SMOKE)	AR	NR	DM	KV
(FORGE, FRODO, ELECT, OCTET/OUGHT/OVERT)	OR	GL	CD/DU/DV	CE/CH/CR
(ORRIS, OCTET/OUGHT/OVERT, SAPPY, TUSSY)	CR/RU/RV	AI	EU/HU/RU	PS
(APING, ASTER, GOURD, RAPID)	PS	NO	AE	IR
(AKUND, AVAST, DONOR, TAKAR)	KV	NO	AS	AO

Some twinned pairs stand out, such as KV and PS. If KV (for instance) is one of the intersecting pairs, then one of the two squares containing it must be a central one. DM is not twinned, so it must be the (AKUND, AVAST, DONOR, TAKAR) square. Chasing up the other pairs in that square, we find that they can indeed all be paired up. We get two options for the NO pair, but when we turn our attention to the PS intersection we are able to resolve that and correctly divide the squares into the two grids. Along the way, the intersections cleared up the uncertainties over the placement of TACKS/TONES and OCTET/OUGHT/OVERT. The only remaining ambiguity is the placement of SHARK and SLICK; this cannot be resolved, so we simply choose one option and hope that it does not matter.