In the 16th century, the naval powers of Europe were engaged in a race to explore and colonise lands previously unknown to Europeans (though many were of course already inhabited), and reap the rewards of the new found resources. They were limited by the accuracy of navigation at sea. Determining latitude was a relatively simple matter of sighting the angle of a star or the sun through a sextant. But because of the daily rotation of the Earth, determining the longitude by sighting a celestial object required knowing the time of day. Mechanical clocks of the era were rendered useless by the rocking of a ship, making this a major problem.
Solving the problem would give such an advantage to the country holding the secret that in 1598 King Philip III of Spain offered a prize of 6000 ducats plus an annual pension of 2000 ducats for life to whoever could devise a means of measuring longitude at sea. In 1610 the prize was still unclaimed, and in that year Galileo Galilei trained his first telescope on Jupiter, becoming the first person to observe the planet’s largest four moons. He studied their movements, and a couple of years later had produced orbital tables that allowed their positions to be calculated months or years in advance. These tables included the times when a moon would slip into Jupiter’s shadow, and be eclipsed, disappearing from view because it no longer reflected sunlight.
Galileo wrote to King Philip in 1616, proposing a method of telling the time at sea by observing the eclipses of Jupiter’s moons. One could pinpoint the time by observing an eclipse, and then use an observation of a star to calculate the longitude. Although the method could work in principle, observing an eclipse of a barely visible object through the narrow field of view of a telescope while standing on a rocking ship was practically impossible, and it never worked in practice.
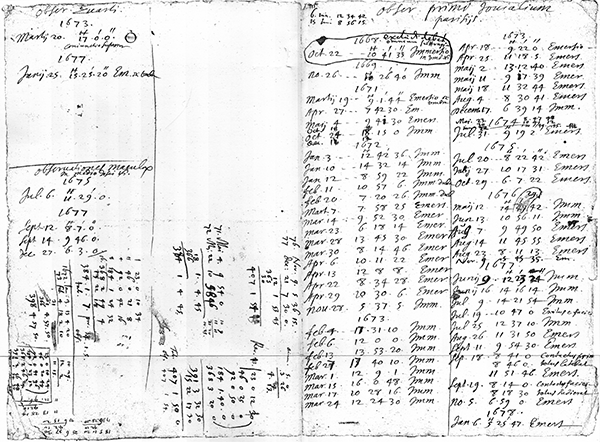
By the 1660s, Giovanni Cassini had developed Galileo’s method as a way of measuring precise longitudes on land, as an aid to calculating distances and making accurate maps. In 1671 Cassini moved to take up directorship of the Royal Observatory in Paris. He dispatched his assistant Jean Picard to Uraniborg, the former observatory of Tycho Brahe, near Copenhagen, partly to make measurements of eclipses of Jupiter’s moon Io, to accurately calculate the longitude difference between the two observatories. Picard himself employed the assistance of a young Dane named Ole Rømer.
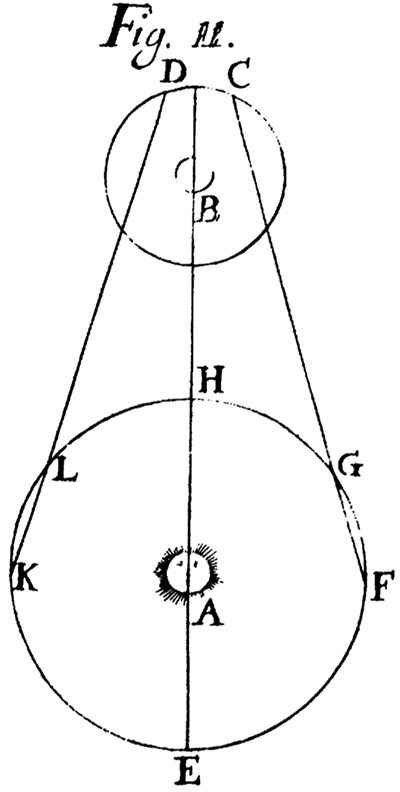
The moon Io orbits Jupiter every 42.5 hours and is close enough to be eclipsed on each orbit, so an eclipse is visible every few days, weather and daylight hours permitting. After observing well over 100 eclipses, Rømer moved to Paris to assist Cassini himself, and continued recording eclipses of Io over the next few years. In these observations Cassini noticed some odd discrepancies. In particular, the time between successive eclipses got shorter when the Earth was approaching Jupiter in its orbit, and longer several months later when the Earth was moving away from Jupiter. Cassini realised that this could be explained if the light from Io did not arrive at Earth instantaneously, but rather took time to travel the intervening distance. When the Earth is closer to Jupiter, the light has less distance to cover, so the eclipse appears to occur earlier, and vice versa: when the Earth is further away the eclipse appears to be later because the light takes longer to reach Earth. Cassini made an announcement to this effect to the French Academy of Sciences in 1676.
However, it was common wisdom at the time that light travelled instantaneously, and Cassini later retreated from his suggestion and did not pursue it further. Rømer, on the other hand, was intrigued and continued to investigate. In 1678 he published his findings. He argued that as the Earth moved in its orbit away from Jupiter, successive eclipses would each occur with the Earth roughly 200 Earth-diameters further away from Jupiter than the previous one. Using the geometry of the orbit and his observations, Rømer calculated that it must take light approximately 11 minutes to cross a distance equal to the diameter of the Earth’s orbit. This is a little low—it actually takes about 16 and a half minutes—but it’s the right order of magnitude. So for the first time, we had some idea how fast light travels. And as we’ve just seen, the finite speed of light can have a significant effect on the observed timing of astronomical observations.
The finite speed of light means that astronomical events don’t occur when we see them. We only see the event after enough time has elapsed for the light to travel to Earth. This is important for events with precisely measurable times, such as eclipses, occultations, the brightness variations of variable stars, and the radio pulses of remote pulsars.
Not only do you need to correct for the time it takes light to reach Earth, but the correction is different depending on where you are on Earth. An observer observing an object that is directly overhead is closer to it than an observer seeing the same object on the horizon. The observer seeing the object on the horizon is further away by the radius of the Earth. The radius of the Earth is 6370 km, and it takes light a little over 21 milliseconds to travel this distance. So astronomical events observed on the horizon appear to occur 21 milliseconds later than they do to someone observing the same event overhead. This effect is significant enough to be mentioned explicitly in a paper discussing the timing of variable stars:
“More disturbing effects become significant which require more conventions and more complex reduction procedures. By far the biggest effect is the topocentric light-time correction (up to 20 msec).”[2]
Topocentric refers to measuring from a specific point on the surface of the Earth. Depending where on Earth you are, the timing of observed astronomical events can appear to vary by up to 20 ms.
Not only does the light travel time affect the observed time of astronomical events, it also affects the observed position of some astronomical objects, most importantly solar system objects that move noticeably over the few hours that light takes to travel to Earth from them. When we observe an object such as a planet or an asteroid, we see it in the position that it was when the light left it, not where it is at the time that we see it. So for such objects, a corrected position needs to be calculated. The correction in observed position of a moving astronomical object due to the finite speed of light is, somewhat confusingly, also known as light time correction.
Light time correction of observed position is critical in determining the orbits of bodies such as asteroids and comets with accuracy. A paper describing general methods for determining orbital parameters from observations notes that Earth-based observations are necessarily topocentric, and states in the description of the method that:
“In the case of asteroid or comet orbits, the light-time correction has been computed.”[3]
Finally, a recent paper on determining the orbital parameters of near-Earth objects (which pose a potential threat of catastrophic collision with Earth) points out, where ρ is the topocentric distance:
“Note that we include a light-time correction by subtracting ρ/c from the observed epochs for any propagation computation with c as speed of light.”[4]
All of these corrections, which must be applied to astronomical observations where either (a) timings must be known to less than a second or (b) positions must be known accurately to determine orbits, are different by a light travel time of 21 ms for observers looking at objects directly overhead versus observers looking towards the horizon. And in between the light time corrections are 21 ms × (1 minus the sine of the observation zenith angle).
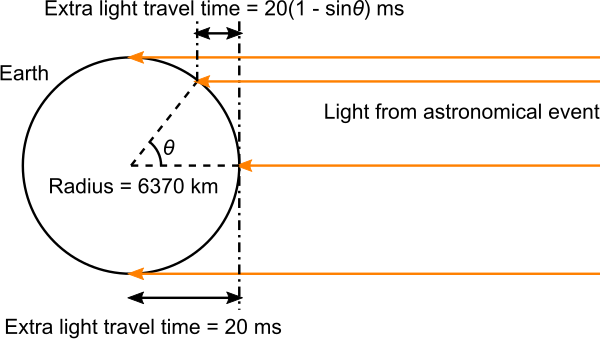
This implies that places on Earth where an astronomical object appears near the horizon are a bit over 6000 km further away from the object than the location where the object is directly overhead. This is true no matter which object is observed, meaning it is independent of which position on Earth is directly under it. This cannot be so if the Earth is flat.
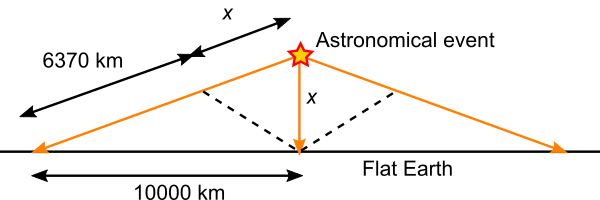
Observation points on Earth where an astronomical event is overhead and on the horizon are separated by 10,000 km. If the Earth is flat, then the geometry must be something like that shown in the diagram above. The astronomical event is a distance x above the flat Earth, such that the distance from the event to a point 10,000 km along the surface is x plus the measured light travel time distance of 6370 km. Applying Pythagoras’s theorem:
(6370 + x)2 = 100002 + x2
Solving for x gives 4660 km. So measurements of light time correction imply that all astronomical events are 4660 km above the flat Earth. This means the elevation angle of the event seen from 10,000 km away is arctan(4660/10,000) = 25°, well above the horizon, which is inconsistent with observation (and the trigonometry of all the intermediate angles doesn’t work either). It’s also easy to show by other observations that astronomical objects are not all at the same distance – some are thousands, millions, or more times further away than others, and they are all much further away than 4660 km.
So the measurement of light time corrections imply that observers on Earth are positioned on the surface of a sphere. In other words, that the Earth is spherical in shape.
References:
[1] Rømer, O. (“A Demonstration Concerning the Motion of Light”.) Philosophical Transactions of the Royal Society, 12, p. 893-94, 1678. (Originally published in French as “Demonstration touchant le mouvement de la lumiere trouvé”. Journal des Sçavans, p. 276-279, 1677.) https://www.jstor.org/stable/101779
[2] Bastian, U. “The Time Coordinate Used in the Variable-star Community”. Information Bulletin on Variable Stars, No. 4822, #1, 2000. https://ui.adsabs.harvard.edu/abs/2000IBVS.4822….1B/abstract
[3] Dumoulin, C. “Unified Iterative Methods in Orbit Determination”. Celestial Mechanics and Dynamical Astronomy, 59, 1, p. 73-89, 1994. https://doi.org/10.1007/BF00691971
[4] Frühauf, M., Micheli, M., Santana-Ros, T., Jehn, R., Koschny, D., Torralba, O. R. “A systematic ranging technique for follow-ups of NEOs detected with the Flyeye telescope”. Proceedings of the 1st NEO and Debris Detection Conference, Darmstadt, 2019. https://ui.adsabs.harvard.edu/abs/2019arXiv190308419F/abstract