Travel in a straight line across the surface of the Earth in any direction. After approximately 40,000 kilometres, you will find you are back where you started, having arrived from the opposite direction. While this sort of thing might be common in the wrap-around maps of some 1980s era video games, the simplest explanation for this in the real world is that the Earth is a globe, with a circumference about 40,000 km.
It’s difficult to see how this sort of thing could be possible on a flat Earth, unless the flat Earth’s surface were subject to some rather extreme directional and distance warping—that exactly mimics the behaviour of the surface of a sphere in Euclidean space. While this is not a priori impossible, it would certainly be an unlikely coincidence. Occam’s razor suggests that if it looks like a duck, quacks like a duck, and perfectly mimics the Euclidean geometry of a duck, it’s a duck.
This could be a very short and sweet entry if I left things there, but there are a few dangling questions.
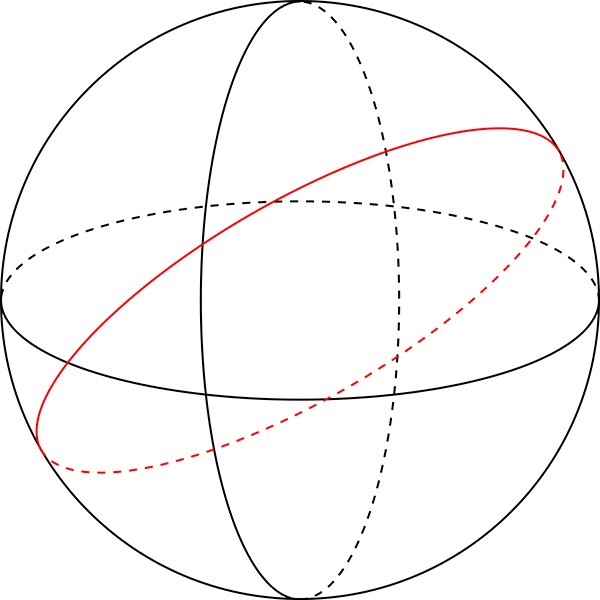
Firstly there’s the question of exactly what we mean by a “straight line”. The Earth’s surface is curved, so any line we draw on it is necessarily curved in the third dimension, although this curvature is slight at scales we can easily perceive. The common understanding of a “straight line” on the Earth’s surface is the line giving the shortest distance joining two points as measured along the surface. This is what we mean when we talk about “straight lines” on Earth in casual speech, and it also matches how we’re using the term here.
In three dimensions, such “straight lines” are what we call great circles. A great circle is a circle on the surface of a sphere that has the same diameter as the sphere itself. On an idealised perfectly spherical Earth, the equator is a great circle, as are all of the meridians (i.e. lines of longitude). Lines of latitude other than the equator are not great circles: if you start north of the equator and travel due west, maintaining a westerly heading, then you are actually curving to the right. It’s easiest to see this by imagining a starting point very close to the North Pole. If you travel due west you will travel in a small clockwise circle around the pole.
Secondly, how can we know that we are travelling in such a straight line? The MythBusters once tested the myth that “It is impossible for a blindfolded person to travel in a straight line” and found that with restricted vision they were unable to either walk, swim, or drive in a straight line over even a very short distance[1]. We don’t need to keep our eyes closed though!
When travelling through unknown terrain, you can navigate by using the positions of the sun and stars as a reference frame, giving you a way of determining compass directions. Converting this into a great circle path however requires geometric calculations that depend on the spherical geometry of the Earth, so this approach is a somewhat circular argument if our aim is to demonstrate that the Earth is spherical.
A more direct method to ensure straight line travel is to line up two landmarks in the direction you are travelling, then when you reach the first one, line up another beyond the next one and repeat the process. This procedure can keep your course reasonably straight, but relies on visible and static landmarks, which may not be conveniently present. And this method is useless at sea.
Modern navigation now uses GPS to establish a position accurate to within a few metres. While this could be (and is routinely) used to plot a straight line course, again this relies on geometrical calculations that assume the Earth is spherical. (It works, of course, because the Earth is spherical, but render this particular line of argument against a flat Earth circular.)
Before GPS became commonplace, there was a different sort of navigation system in common use, and it is still used today as a backup for times when GPS is unavailable for any reason. These older systems are called inertial navigation systems (INS). They use components that provide an inertial frame of reference—that is, a reference frame that is not rotating or accelerating—independent of any motion of the Earth. These systems can be used for dead reckoning, which is navigating by plotting your direction and speed from your starting location to determine where you are at any time. They can be used to ensure that you follow a straight line path across the Earth, with reference to the inertial frame.
Inertial navigation systems can be built using several different physical principles, including mechanical gyroscopes, accelerometers, or laser ring gyroscopes utilising the Sagnac effect (previously discussed in these proofs). These systems drift in accuracy over time due to mechanical and environmental effects. Modern inertial navigation systems are accurate to 0.6 nautical miles per hour[2], or just over 1 km per hour. A plane flying at Mach 1 can fly a great circle route in just over 32 hours, so if relying only on INS it should arrive within 32 km of its starting point, which is close enough that a pilot can figure out that it’s back where it started. So in principle we can do this experiment with current technology.
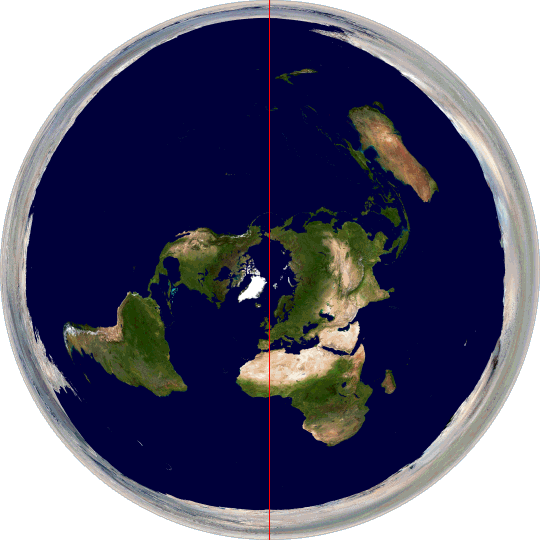
A great circle on our spherical Earth is straightforward. But what does a great circle path look like plotted on a hypothetical flat Earth? Here are a few:
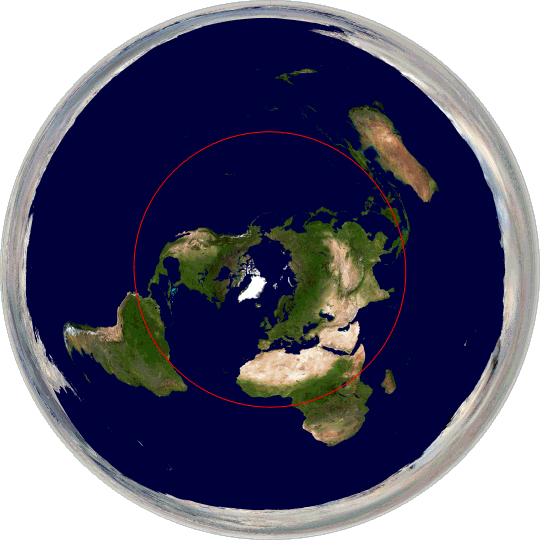

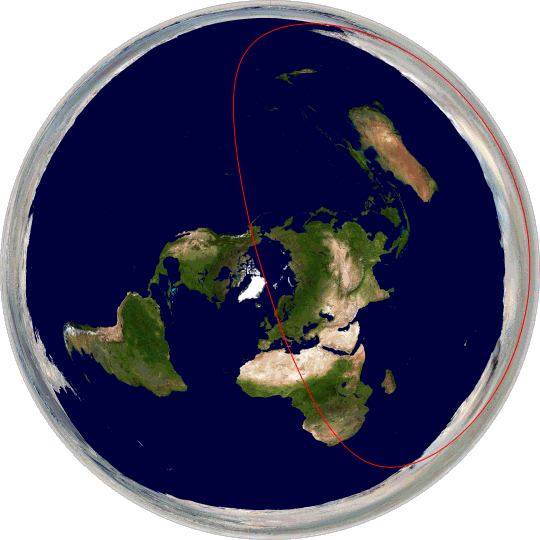
As you can see, great circle paths are distorted and misshapen when plotted on a flat Earth. If you follow a straight line across the surface of the Earth as given by inertial navigation systems there’s no obvious reason why you would end up tracing any of these paths, or why you would measure the same distance travelled (40,000 km) over all three paths when they are significantly different sizes on this map. And then consider this one:
This circle passes through the north and south poles. If you travel on this great circle, then you have to go off one edge of the flat Earth and reappear on the other side. Which seems unlikely.
Travelling in a straight line and ending up where you started makes the most sense if the Earth is a globe.
References:
[1] “MythBusters Episode 173: Walk a Straight Line”, MythBuster Results, https://mythresults.com/walk-a-straight-line (accessed 2019-08-20).
[2] “Inertial Navigation System (INS)”, Skybrary, https://www.skybrary.aero/index.php/Inertial_Navigation_System_(INS) (accessed 2019-08-20).
…Now I’m imagining “Proof xx: Amundsen-Scott Station”.
(We haven’t had that one yet, right? I hadn’t actually checked.)
Oh, right, number 9, I guess. Though it’s kind of missing a reference to the actual station.
I know this blog isn’t meant to convince flat Earthers, but I always wonder why they can show up in huge groups for giant “shoot lasers across a lake” experiments that they misinterpret, but none of them can spend a few days driving and seeing how driving directions work on a globe but not a flat plane.
“If you travel due west you will travel in a small anticlockwise circle around the pole.”
Don’t you mean clockwise?
“Lines of latitude other than the equator are not great circles: if you start north of the equator and travel due west, maintaining a westerly heading, then you are actually curving to the right.”
Does that really matter though? Whether you’re following a great circle or not, you still end up back where you started. And you shouldn’t need any special method or equipment to travel in a straight line, as long as you have a compass and maintain a constant heading.
Of course, a Flat Earther would say that when you travel due West or East, you’re actually following a circular path, not a straight line. The real proof is that it takes the same amount of time to circumnavigate the Earth at X degrees North as it does at X degrees South (assuming a fixed speed).
Clockwise, yes, oops. Thanks, I’ve fixed that.
What matters about curving right is that if you curve right then you also end up back where you started on a flat Earth, because you travel in a circle. So it’s important for this proof that you travel in a straight line without curving.