CiSRA Puzzle Competition 2013 - Solutions

3E. Sudorubikube

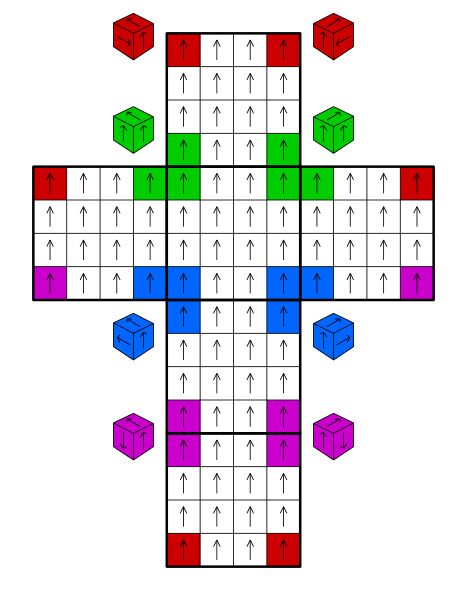
The title of this puzzle hints at its nature: it's a Sudoku wrapped around a 4×4×4 Rubik's Cube (or Rubik's Revenge), which has then been scrambled. Here's the original presentation of the puzzle:

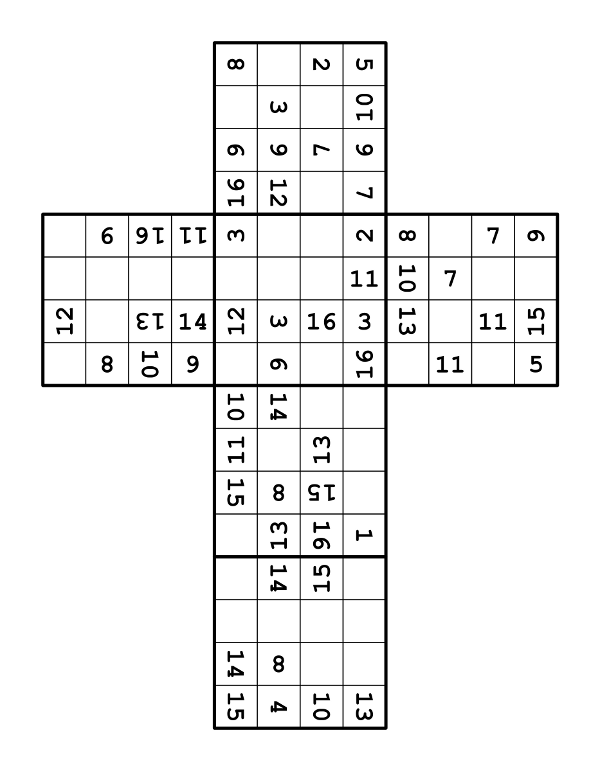
Some assumptions are necessary to solve the puzzle:

• The Rubik's Cube has been scrambled using ordinary turns of the faces and inner slices.
• The Sudoku uses the numbers 1 to 16. (These numbers are all given in the puzzle, and the faces are 4×4.)
• The unscrambled Sudoku will have all of its numbers upright in the unfolded cube net shape given in the puzzle (shown as the arrows shown in the diagram below).
• The Sudoku-on-a-cube follows the normal rules of Sudoku. (I.e. each row, column, and face of the cube must contain the numbers 1 to 16. Rows and columns wrap around the cube, spanning four faces each, as shown below.)

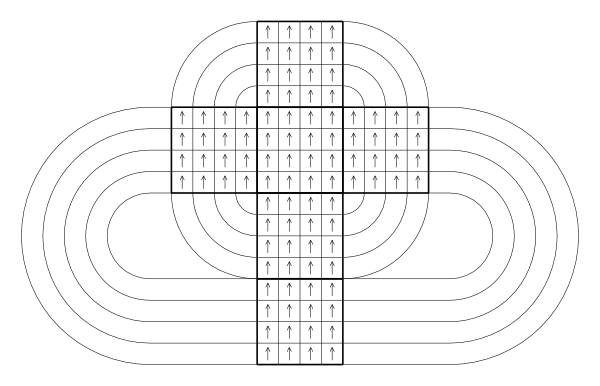
The first step is to unscramble the cube into a valid Sudoku-on-a-cube, as per the above assumptions. The difficulty of unscrambling is compounded somewhat by the fact that the 6 and 9 characters used are rotationally equivalent to each other, as well as 8s which have rotational symmetry.

It's possible to unscramble the cube by sticking labels onto an actual 4×4×4 Rubik's Cube, and playing with it until none of the assumptions are violated (there is only one such configuration), however this approach is a little ad-hoc. The intended method of unscrambling is to deduce various properties of the puzzle form, and use them to put together the unscrambled puzzle piece by piece. Some details of this approach are given further down as an appendix.

The unscrambled Sudoku looks like this:

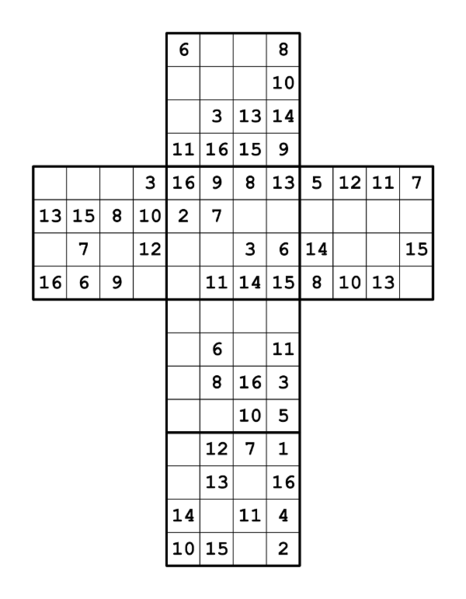
From here, it's possible to use ordinary Sudoku solving methods (albeit on a cube) to solve the Sudoku and provide the missing numbers. Here's the completed Sudoku:

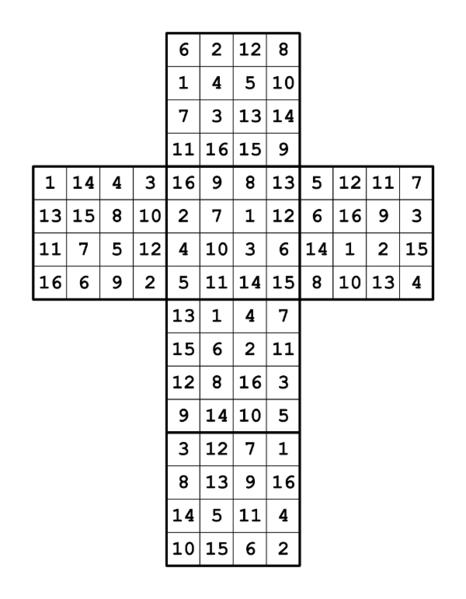
By converting numbers to letters, assuming 1 is A, 2 is B and so on up to 16 is P, the Sudoku can be viewed as a collection of letters. However, although a few simple words appear there's nothing immediately compelling:

The next step requires an intuitive leap to surmise that the numbers that were missing at the start of the puzzle should be treated differently from the ones that were given. If you unscrambled the cube first, and then filled in the missing Sudoku numbers with a different colour, for example, these numbers may be easy to separate. However it's also possible to solve some of the Sudoku numbers while still unscrambling the cube, in which case the separation can become muddied. Even so, you can still uniquely determine the difference by making use of the observation that an upright number can be located within only six places in the puzzle.

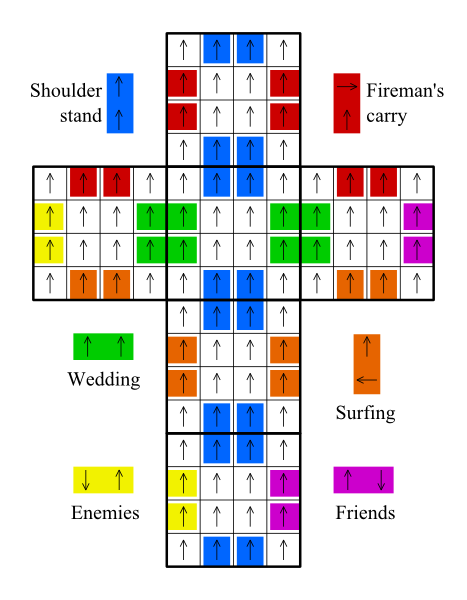
Either way you resolve the issue, shading the numbers by whether they were provided or had to be filled in reveals a secret message in the missing numbers (shown in white below):

The message reads: BLADE GANDALF PICKED JABBED MAD GOBLIN CHIEF.

In the Lord of the Rings books and movies, Gandalf used the sword Glamdring, picked from a troll's cache, to smite the Great Goblin under the Misty Mountains. GLAMDRING is the answer to the puzzle. We also accepted FOE HAMMER, which is the meaning of the name given by the elves to the weapon, or BEATER, the name given by the orcs and goblins to the same blade.

Appendix: Unscrambling on paper

The orientations of the arrows can reveal features of this puzzle that will help a solver to place the scrambled pieces back into their original unscrambled positions.

The three numbers on a corner cubelet are joined on a single solid piece, and cannot be separated from each other by any twist performed on the cube. For example, the numbers 11, 16, and 3 in the corner between the left, upper, and front faces all belong to the same corner piece. The 11 will always be to the right of the 3 and above the 16.

Looking at the central four faces running from the top to the bottom of the unfolded cube net, it can be seen that every corner cubelet consists of one upright number sitting atop another upright number. For the numbers on the left or right side that form the third face of that cubelet, there are instances of all four orientations down the length of the cube. Importantly, every cubelet's set of three numerical orientations is unique, and so any corner piece whose three numerical orientations are certain can immediately be assigned to its position in the unscrambled puzzle:

Edge cubelets consist of only two solidly joined numbers. For example, in the given puzzle the number 10 at the very bottom of the puzzle cannot be separated from or changed in orientation relative to the number 2 that's at the very top of the puzzle - they're stuck together on the same solid piece.

For edge cubelets with known numerical orientations, the possible placements are limited:

A further property of any given number in the puzzle is that the number can only possibly occupy four possible positions on any face, and in general, only one of those positions on the face is upright. For example, there are only four positions that the 12 below can be moved into within its current face.

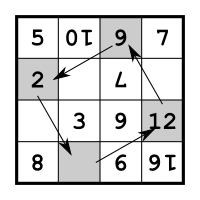
No twists of the cube, including shifting the edge piece with the 12 off the face, and back on again from a different direction, can put the 12 into a position on the face other than the four positions (and orientations) that can be reached by directly rotating the face. This applies equally to numbers on corner, edge, and face cubelets.

This leads to a powerful deduction: if the orientation of a number is certain, there are only six locations in the entire puzzle where that number can appear (one spot within the 4×4 grid of each face).

These deductions, combined with the rules of Sudoku, can be used to produce an unscrambled version of the puzzle just by inspection and logic.

Puzzle design notes:

Although I originally considered a Doctor Who theme for the secret in this puzzle, I found the choice of words very limited because of the constraint that they had to use only the first 16 letters of the alphabet ("Dalek" being one of the few that seemed reasonable). So I started looking through words that can be formed entirely from the letters A to P to see what else might be possible.

A number of words stood out to me, including words such as: MAGIC OLD HIGH ELF BLADE CLOAKED MAGE IMPALED GOBLIN KING ON AND HELD BACK FLAMING DEMONIC BANE.

I then quickly realised that GANDALF, BILBO, and several dwarven names also fitted the bill, which provided the specificity needed to produce a unique answer to the puzzle. Unfortunately both GANDALF and BILBO repeated letters and so constrained the secret to write those words broken apart. This led to the letters of the secret being scattered through the puzzle, meaning they had to be represented by the empty squares so that they could be located in the end.

(This produced a slight weakness in the puzzle - it was susceptible to a frequency analysis and anagram attack - however this was considered an acceptable risk given the use of an unusual proper name within the secret.)

Another constraint was that a Sudoku cannot give away all instances of a number, so the secret message needed to use at least one instance of each of the letters from A to P. It turned out that using a J was a significant constraint, which led to the word JABBED being used instead of IMPALED.

For those who want a harder challenge, here's an earlier version of the puzzle:

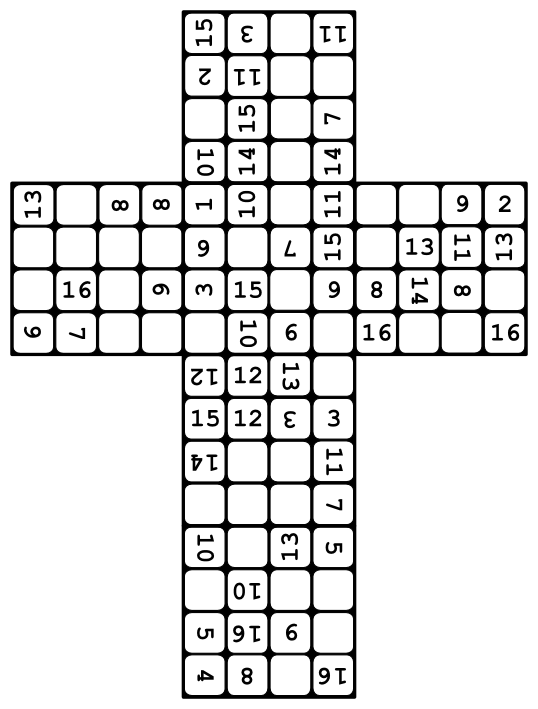
Enjoy!

Thanks

Extra special thanks to Geoff Bailey for many insights and discussions on the structure and possibilities of this puzzle. He really helped develop this puzzle beyond the simple extension of a Sudoku puzzle onto a cube into a more fully three dimensional puzzle.