
CiSRA Puzzle Competition 2013 - Solutions
2D. Look, Ma!
Many aspects of the puzzle - the twelve dots, the Roman numeral XI, the circles with 0°, 30°, 60°, and 90° angle lines - hint at the puzzle involving clocks somehow. The puzzle title evokes the famous phrase "Look, Ma! No hands!". So treating the puzzle as a clock missing its hands is a good assumption.
But what do the sun and moon dots mean? The moon dot marked XI is interesting. If you mark clock times around the two circles, the XI dot is directly above 11 on the smaller circle, and the distance above that point is exactly the distance of one radius of the larger circle. Equivalently, you can picture it as the missing hour hand going from the centre dot to the 11 o'clock position on the small circle, and the minute hand going from the 11 to the XI (instead of its usual position from the centre of the circle to the 12 o'clock position on the outer circle).
The dots, in other words, represent clock times by the position of the end of the minute hand as if the minute hand were attached to the end of the hour hand, rather than to the centre of the clock.
But wait! Imagine a parallelogram using two different pairs of hour and minute hands, joining the centre dot and a sun or moon dot. There are two possible clock hand positions for each dot! However, both of these positions do not necessarily represent valid times. For example, if the minute hand is pointing due north, the hour hand must be pointing in the direction of one of the twelve hour markings.
It requires some precision work (we recommend printing out the puzzle fairly large), but it's possible to work out the representative time for each dot, shown graphically below. Each red dot shows the position of the hour hand, and the attached red line shows the direction of the minute hand, connecting the red dot and a sun/moon dot. To see the corresponding time, imagine the red line moved parallel to itself so that it begins at the centre of the circle.
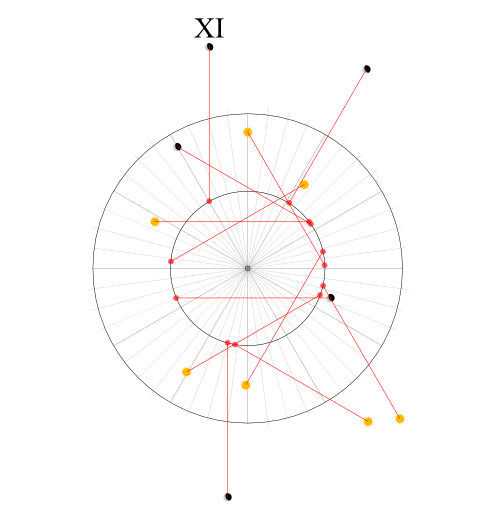
Listing the times associated with each dot from top to bottom, the times are:
| 11:00 | |
| 1:05 | |
| 2:55 or 9:05 (ambiguous) | |
| 1:50 | |
| 9:10 (also close to 5:05) | |
| 1:45 (also close to 9:55 | |
| 8:15 | |
| 3:40 | |
| 2:35 (also close to 9:25) | |
| 3:25 | |
| 6:20 | |
| 6:30 |
It may become apparent while solving that the minute parts of all the times are at five minute intervals. Compellingly, all twelve such intervals within the hour (:00, :05, etc) are represented, if the ambiguous time is correctly interpreted as 2:55, rather than 9:05. This fact also suggests sorting the times according to minute order.
The meaning of the suns and moons remains to be deduced. Logically, the sun is daytime and the moon is nighttime. This indicates that we should care about the difference between AM and PM, suggesting we should be using 24 hour time. The times can be assigned assuming an idealised evenly divided day, with a sunrise at 6:00am and a sunset at 6:00pm. Listing the 24 hour times sorted by minute order as indicated above, and converting the hour numbers to letters, gives the following:
| 12-hr | 24-hr | ||
|---|---|---|---|
| 11:00 | 23:00 | W | |
| 1:05 | 01:05 | A | |
| 9:10 | 09:10 | I | |
| 8:15 | 20:15 | T | |
| 6:20 | 06:20 | F | |
| 3:25 | 15:25 | O | |
| 6:30 | 18:30 | R | |
| 2:35 | 14:35 | N | |
| 3:40 | 15:40 | O | |
| 1:45 | 13:45 | M | |
| 1:50 | 01:50 | A | |
| 2:55 | 14:55 | N |
The given phrase WAIT FOR NO MAN is part of the aphorism TIME AND TIDE WAIT FOR NO MAN.
The answer, as hinted by the presence of the sun (time) and moon (tide) is TIME AND TIDE.
Puzzle design notes:
There is also an aphorism "time waits for no man", but the explicit spelling of the phrase "wait for no man" without the "s" excludes the word TIME by itself as a valid answer.
For those curious about the possible positions of the sun/moon dots, here is a plot showing the locus of the points defined by the vector sum of the hour and minute hands, through a full 12 hour cycle, with the puzzle dot positions marked on the locus.
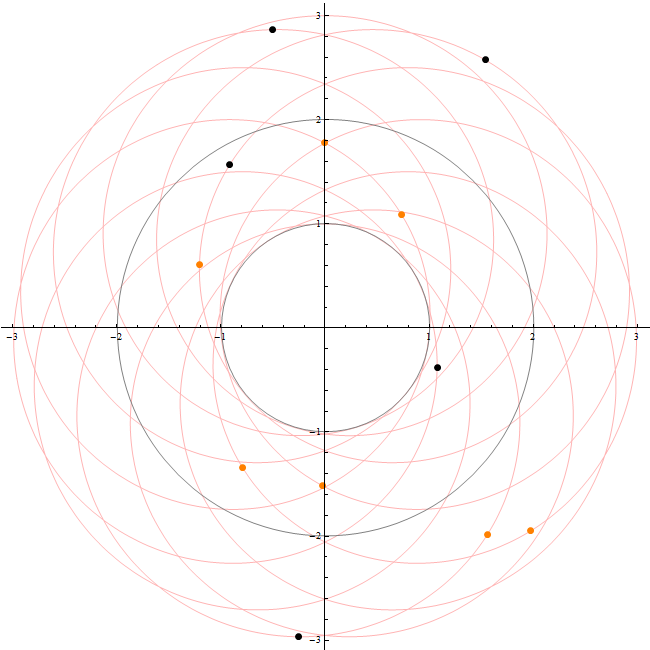
The 2:55 sun dot is at the intersection of two sweeps of the locus, showing its ambiguity with the time 9:05. Most of the other dots are well separated from any ambiguities, but the 9:10, 1:45, and 2:35 dots can be seen to be quite close to intersection points. Doing the construction carefully will resolve any ambiguity for these points (as should the observation that the minute parts of the times are evenly spaced at five minute intervals).