CISRA Puzzle Competition 2012 - Solutions

4C. Blaising Sun

This puzzle resembles puzzle 3D Pyramid Trap, only without any of the clues. There are two independent paths to this puzzle's solution. One gives the answer but does not make it completely clear that it is the answer, while the other makes it umabiguously clear what the answer is once you know it, but is almost impossible to actually identify the answer from without specialised knowledge. Each is described below.

First, the colours. The set of colours present provides something of a clue: Black, Red, Green, Blue, Cyan, Magenta, Yellow, White.

These are the additive (light) primaries, the subtractive (paint) primaries, and the two other extremes in black and white. The insight is that there are actually three overlapping images being encoded by these eight colours. One in each of the additive primary colours - red, green, and blue. Where two images overlap, the subtractive primaries appear - red+green=yellow, green+blue=cyan and blue+red=magenta. White is where all three appear, and black where none appear. That the colours are adding on top of a black base is slightly hinted at by the all-black smaller pyramid. Splitting into these three colour planes yields some fairly compelling structures (in canonical red-green-blue order):

Collecting the symbols from each colour plane gives the following:

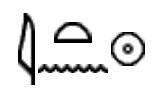
But what do they mean? Any team with an Egyptologist may have solved the puzzle from this, but the rest of us need to turn to the numbers.

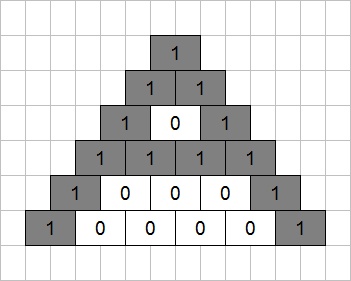
The small pyramid is provided as an easier warm-up version of the large pyramid. The title of the puzzle provides a critical clue for what to do. The word "Blaise" suggests the mathematician Blaise Pascal, who among other things is known for Pascal's Triangle. Pascal's Triangle is a similarly shaped triangle of numbers, formed by the rule that each number is the sum of the two directly above it.

So, does that rule hold for this triangle? It does in some places but not others. There are two exceptions: Some numbers are one greater than the sum of the two above, while others are ten smaller. The latter exception, along with the observation that no pyramid has a number larger than 9, suggests working in modulo ten. In modulo ten, all numbers in the small pyramid are either the sum of the two above, or one greater than the sum of the two above. Marking the bricks which are one greater makes a capital "A" shape, helping confirm that this is the right track:

Repeating the same process on the large pyramid gives a set of numbers which are all between 0 and 7 (inclusive):

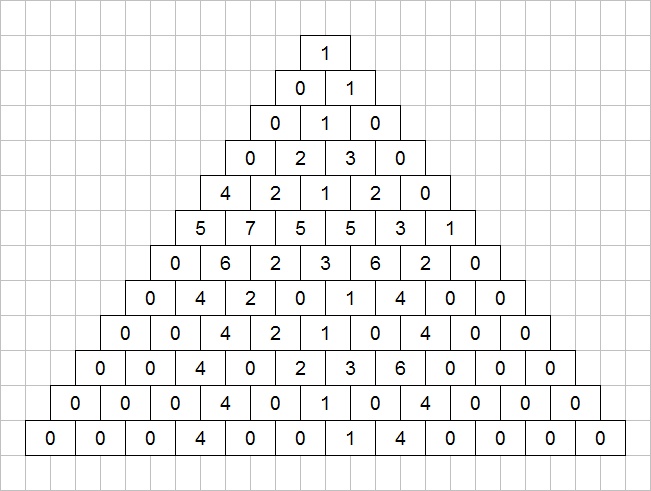
In the same way as the eight colours were separated into red, green, and blue, the numbers 0 to 7 are now separated into the binary powers 1, 2, and 4. This yields three lower case letters:

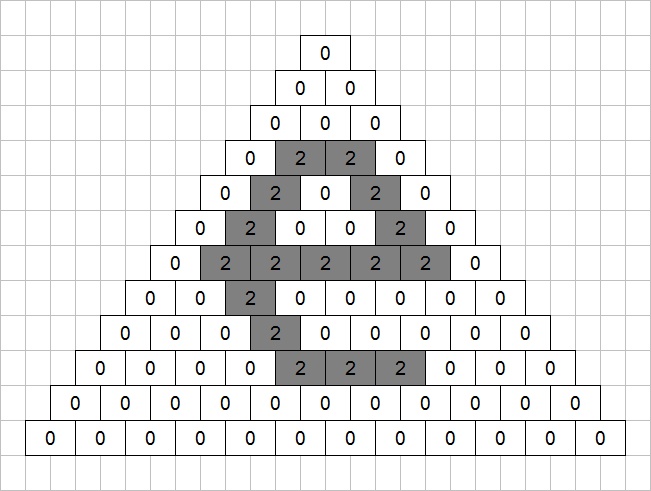
The "A" being upper case suggests putting it at the start, and the remaining letters spell either "ten" or "net" depending on how they are ordered. "ten" could be a clue to work modulo ten, but it's a little late to find that out! Now, though, there are hopefully enough clues to identify the answer: ATEN. Aten was worshipped as a sun god by ancient Egyptians (further confirmed by the word "Sun" in the title). The meaning of the symbols produced by the colour separations can now also be confirmed as Aten's name in hieroglyphs.