CISRA Puzzle Competition 2012 - Solutions
3C. Shape Sorter
The title of the puzzle as well as the presentation suggest a popular child's toy known as a "shape sorter". Such a toy consists of a box with various shaped holes in it and a set of prismic shaped objects. In order to get the objects into the box, the child needs to recognise that the shape of the holes matches the shape of the objects, and the each object will only fit in the matching hole. Often the shapes and the outside of the holes have matching colours as well to make things easier for them. Of course, the first thing any "older kid" (a term which stretches all the way to many adults) does is try and outsmart the toy and work out how to jam the shapes into the wrong holes, with a combination of turning them sideways or on awkard angles and the use of excessive force. This puzzle is based around that theme.
It can be seen that the colours of the shapes match up to the colours of the "right" holes. Right in the sense that they are a shape with the same name at least. However it's quite clear that the shapes don't fit at all in the "right" holes. Although they are basically the same shape, they're distorted in various ways (mostly by stretching). Incidentally, the colour matching is redundant in that the shapes could be matched to the right holes by name, the colours just confirm that mapping.
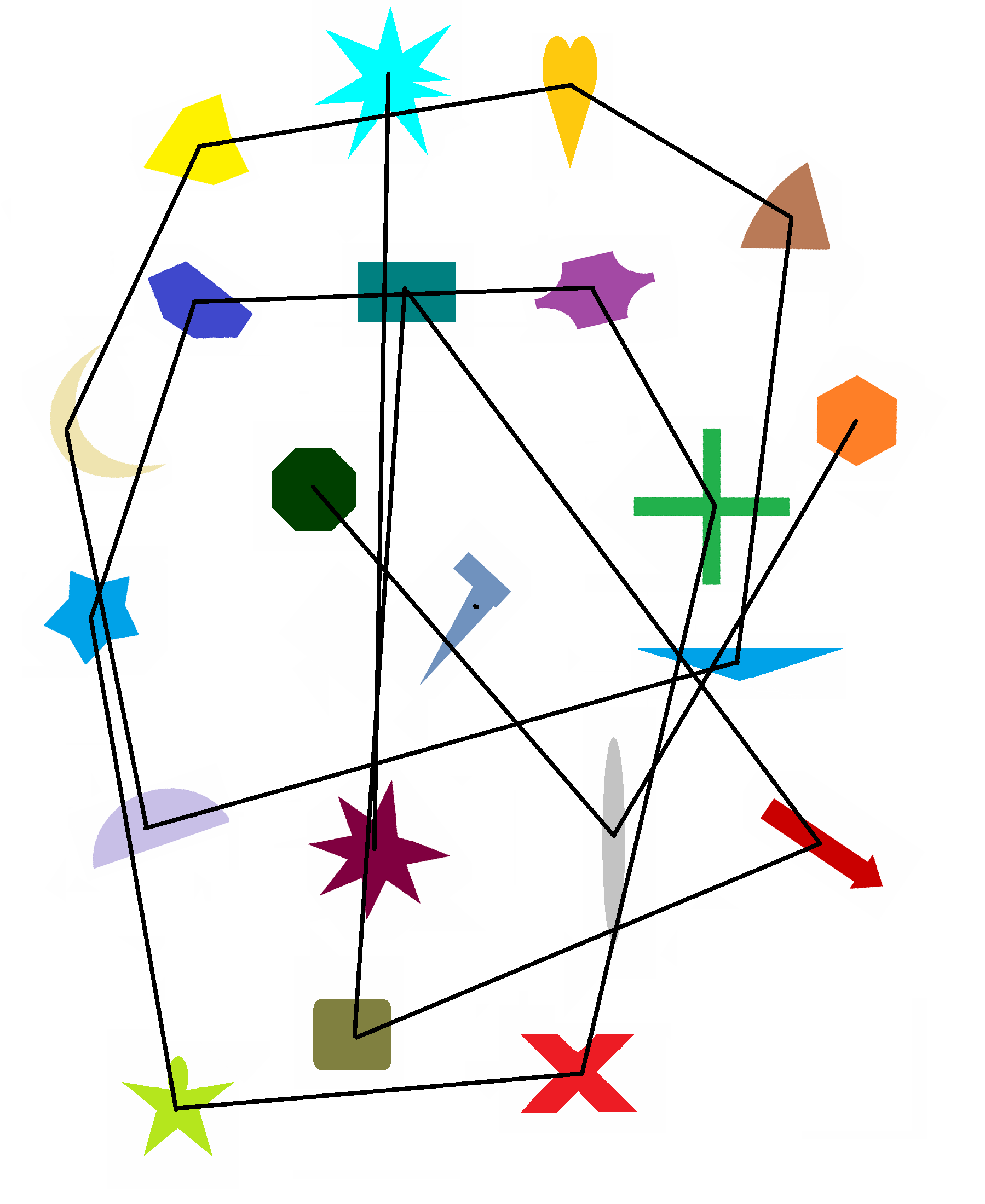
The trick to the puzzle is to try and get the shapes into the box by sticking them into the "wrong" holes. It can be seen that for the most part each shape will only fit into one of the holes. The following image shows the shapes superimposed over the holes that they fit into (this was the source image from which the puzzle was built). Note the colours are the wrong way around (the shape is black and the hole is the appropriate colour) and this does not include the coloured rings around the holes (which were added later).

Cutting the shapes out helps a lot, though you would want to be pretty precise with the scissors. Some other shape-hole combinations come very close to fitting, but quite a bit of painstaking effort was put into making sure other combinations didn't quite fit. There are still a couple of oddities: The ellipse shape fits into both the hexagon and the octagon holes, and symmetrically the hexagon and octagon both fit into the circular (i.e. elliptical) hole. Also, the callout shape is special for the fact that it actually does fit in its own hole, although it needs to be turned sideways to do so.
The next step requires thinking in terms of chains of which shape fits into which hole. For instance, the rectangle shape fits inside the arrow hole, the arrow shape fits inside the round-rectangle hole, and the round-rectangle shape fits inside the rectangle hole, forming a loop of three. Altogether, the following loops are formed:
- heart -> sector -> triangle -> segment -> moon -> chevron -> heart
- hexagon -> ellipse -> octagon -> ellipse -> hexagon
- plaque -> plus sign -> "x" -> person -> 5 point star -> pentagon -> plaque
- 7 point star -> 8 point star -> 7 point star
- rectangle -> arrow -> round rectangle -> rectangle
- callout -> callout (the shape made of a rectangle attached to a triangle)
Drawing these chains onto the box itself yields the following:

From this you can read another shape name (the letters are close to being in order though not quite), which is the answer to the puzzle: OVOID
Incidentally, drawing them on the shapes works as well, though less neatly: