CiSRA Puzzle Competition 2010 - Solutions

3D. Art

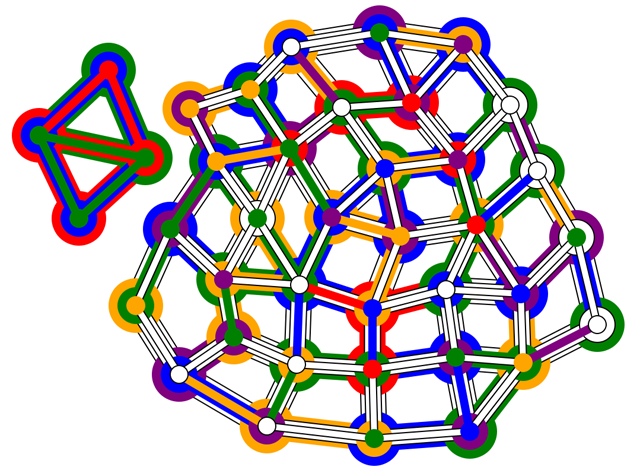
This puzzle shows an incompletely coloured illustration, and a smaller completed illustration to its left. The main challenge of the puzzle is deriving the rules that allow the puzzle to be coloured, with no ambiguities or contradictions.

From the example on the left, some simple rules can be hypothesised.

There appear to be three layers of lines and circles, all containing continuous areas of colour. Every area of colour spans several lines and circles. A compelling "first try" rule might be that you can't have a line by itself (it has to connect to a circle of the same colour). From the red lines and circles in the example, a line can connect to a circle at the same layer or one below - in other words, wherever the shapes actually touch one another in the 2D drawing. From the green lines and circles, the same colour can exist on the same line or circle on two different layers.

Can the same colour exist on adjacent lines or circles? The example doesn't show any, and colouring usually doesn't have adjacent regions being the same colour. It's a reasonable hyphothesis that you can't.

Using these tentative rules, you can already do some colouring. For example:

In the above extract, you can colour the left outer circle green (otherwise the adjacent outer green line doesn't connect to anything green) and the outer right circle blue (for a similar reason).

In fact, using this rule alone, you can colour many of the circles - almost all in the bottom layer, many middle ones, and a few top circles. But some circles are still ambiguous, and the rule doesn't say anything about how to colour lines.

Now we need a rule for colouring lines. Looking at the example on the left, you may notice that every circle connects with at least two lines of the same colour. This is also consistent with the colouring done so far. Some more colouring can be done with this rule.

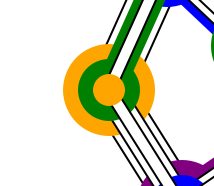
If each circle must have at least two lines of the same colour, any part of the puzzle that has a node with only two joins is completely constrained.

After applying this rule, we get the following:

As you apply this rule, you may begin to notice that "a circle connects with at least two lines" can be specified more strictly as "a circle connects with exactly two lines". This is the final rule that allows the rest of the puzzle to be coloured in.

In summary, the rules are:

• Each line has at least one circle of the same colour touching it.
• Each circle has exactly two lines of the same colour touching it.
• A line touches a circle if the circle is at the same level or one lower. (i.e. if the areas on the page are touching)
• Adjacent circles and adjacent lines can't be the same colour.

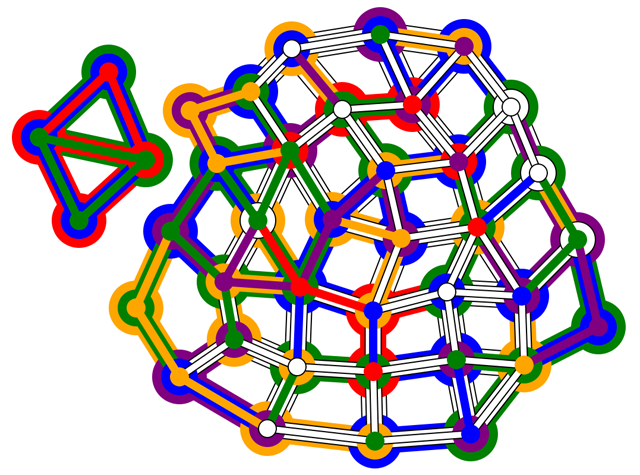
By using these rules, the entire puzzle can be coloured consistently and unambiguously.

When the image is completely coloured, the red sections make the shape of an interesting looking symbol.

This is the alchemical, astrological, and astronomical symbol for MERCURY.