CiSRA Puzzle Competition 2010 - Solutions

2D. The Lay of the Stars

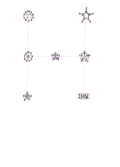
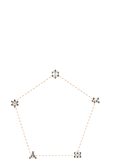
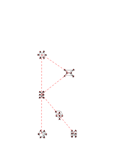
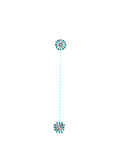
This puzzle contains a collection of symmetric graphs, with 6 to 12 nodes and 3 or 4 edges at each node. In fact, they're all regular graphs, meaning they have the same number of edges connecting to each node.

Many of the graphs in this puzzle are isomorphic to each other, meaning that they are mathematically the same graph, but arranged differently. i.e. They can be stretched into the same shape without breaking any of the edges. Working out exactly which graphs are isomorphic is a difficult step, as there are graphs which have the same number of nodes and edges but are not isomorphic to one another.

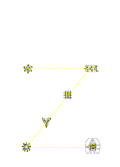
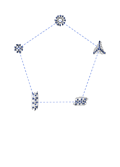
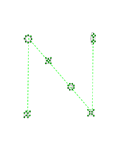
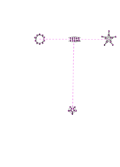
The sets of isomorphic graphs are shown in the diagram below, identified by colour.

Each set of isomorphic graphs forms a letter. The images below show this, with dashed lines added to show the letters they form. In each of the graphs, the nodes are numbered to show how they map to one another isomorphically (click to get the large versions to see this).

The graphs and the letters they produce are:

Colour	Description	Name	Letter
Red	6 nodes, 9 edges	K3,3 or the utility graph	R
Brown	6 nodes, 9 edges	Triangular prism graph	O
Green	8 nodes, 12 edges	Cubical graph	N
Yellow	9 nodes, 18 edges	Triangles joined by triangles	Z
Orange	9 nodes, 18 edges	(1,2) circulant graph	A
Grey	9 nodes, 18 edges	(1,3) circulant graph	L
Pink	10 nodes, 15 edges	Petersen graph	H
Magenta	10 nodes, 15 edges	Pentagonal prism graph	T
Blue	12 nodes, 24 edges	3 squares connected by 4 triangles	O
Cyan	12 nodes, 24 edges	(1,5) circulant graph	I

The letters anagram to produce the word HORIZONTAL.