Tag: surveying

19. Bridge towers

When architects design and construction engineers build towers, they make them vertical. By “vertical” we mean straight up and down or, more formally, in line with the direction of gravity. A tall, thin structure is most stable if built vertically, as then the centre of mass is directly above the centre of the base area.

If the Earth were flat, then vertical towers would all be parallel, no matter where they were built. On the other hand, if the Earth is curved like a sphere, then “vertical” really means pointing towards the centre of the Earth, in a radial direction. In this case, towers built in different places, although all locally vertical, would not be parallel.

The Humber Bridge spans the Humber estuary near Kingston upon Hull in northern England. The Humber estuary is very broad, and the bridge spans a total of 2.22 kilometres from one bank to the other. It’s a single-span suspension bridge, a type of bridge consisting of two tall towers, with cables strung in hanging arcs between the towers, and also from the top of each tower to anchor points on shore. (It’s the same structural design as the more famous Golden Gate Bridge in San Francisco.) The cables extend in both directions from the top of each tower to balance the tension on either side, so that they don’t pull the towers over. The road deck of the bridge is suspended below the main cables by thinner cables that hang vertically from the main cables. The weight of the road deck is thus supported by the main cables, which distribute the load back to the towers. The towers support the entire weight of the bridge, so must be strong and, most importantly, exactly vertical.

The Humber Bridge

The Humber Bridge from the southern bank of the Humber. (Public domain image from Wikimedia Commons.)

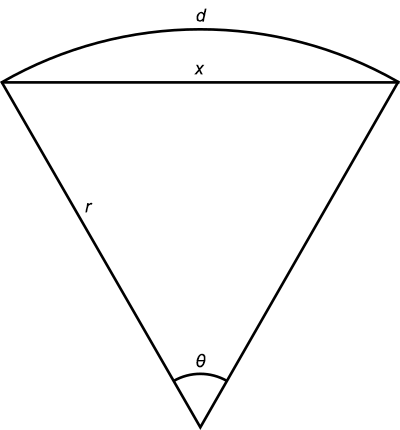
The towers of the Humber Bridge rest on pylons in the estuary bed. The towers are 1410 metres apart, and 155.5 metres high. If the Earth were flat, the towers would be parallel. But they’re not. The cross-sectional centre lines at the tops of the two towers are 36 millimetres further apart than at the bases. Using similar triangles, we can calculate the radius of the Earth from these dimensions:

Radius = 155.5×1410÷0.036 = 6,090,000 metres

This gives the radius of the Earth as 6100 kilometres, close to the true value of 6370 km.

Size of the Earth from the Humber Bridge

Diagram illustrating use of similar triangles to determine the radius of the Earth from the Humber Bridge data. (Not to scale!)

If this were the whole story, it would pretty much be case closed at this point. However, despite a lot of searching, I couldn’t find any reference to the distances between the towers of the Humber Bridge actually being measured at the top and the bottom. It seems that the figure of 36 mm was probably calculated, assuming the curvature of the Earth, which makes this a circular argument (pun intended).

Interestingly, I did find a paper about measuring the deflection of the north tower of the Humber Bridge caused by wind loading and other dynamic stresses in the structure. The paper is primarily concerned with measuring the motion of the road deck, but they also mounted a kinematic GPS sensor at the top of the northern tower[1].

GPS sensor on Humber Bridge north tower

Kinematic GPS sensor mounted on the top of the north tower of the Humber Bridge. (Reproduced from [1].)

The authors carried out a series of measurements, and show the results for a 15 minute period on 7 March, 1996.

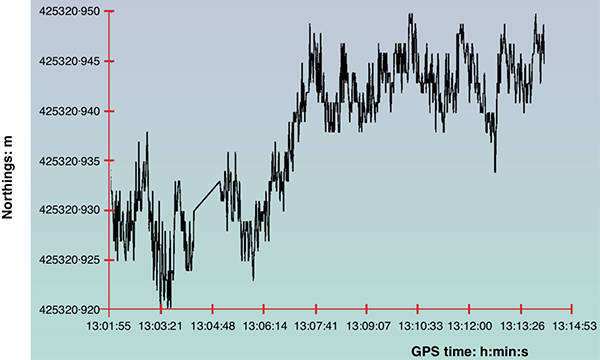
Deflections of Humber Bridge north tower

North-south deflection of the north tower of the Humber Bridge over a 15 minute period. The vertical axis is metres relative to a standard grid reference, so the full vertical range of the graph is 30 mm. (Reproduced from [1].)

From the graph, we can see that the tower wobbles a bit, with deflections of up to about ±10 mm from the mean position. The authors report that the kinematic GPS sensors are capable of measuring deflections as small as a millimetre or two. So from this result we can say that the typical amount of flexing in the Humber Bridge towers is smaller than the supposed 36 mm difference that we should be trying to measure. So, in principle, we could measure the fact that the towers are not parallel, even despite motion of the structure in environmental conditions.

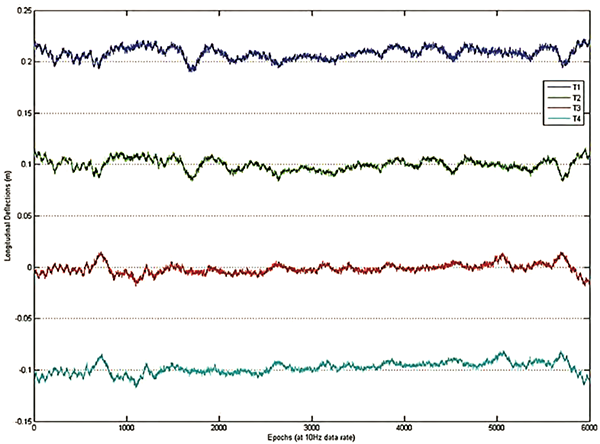
A similar result is seen with the Severn Bridge, a suspension bridge over the Severn River between England and Wales. It has a central span of 988 metres, with towers 136 metres tall. A paper reports measurements made of the flexion of both towers, showing typical deflections at the top are less than 10 mm[2].

Deflections of Severn Bridge towers

Plot of deflection of the top of the suspension towers along the axis of the Severn Bridge. T1 and T2 (upper two lines) are measurements made by two independent sensors at the top of the west tower; T3 and T4 (lower lines) are measurements made by sensors on the east tower. Deflection is in units of metres, so the scale of the maximum deflections is about 10 mm. (Reproduced from [2].)

Okay, so we could in principle measure the mean positions of the tops of suspension bridge towers with enough precision to establish that the towers are further apart at the top than the base. A laser ranging system could do this with ease. Unfortunately, in all my searching I couldn’t find any citations for anyone actually doing this. (If anyone lives near the Humber Bridge and has laser ranging equipment, climbing gear, a certain disregard for authority, and a deathwish, please let me know.)

Something I did find concerned the Verrazzano-Narrows Bridge in New York City. It has a slightly smaller central span than the Humber Bridge, with 1298 metres between its two towers, but the towers are taller, at 211 metres. The tops of the towers are reported as being 41.3 mm further apart than the bases, due to the curvature of the Earth. There are also several citations backing up the statement that “the curvature of the Earth’s surface had to be taken into account when designing the bridge” (my emphasis).[3]

Verrazzano-Narrows Bridge

Verrazzano-Narrows Bridge, linking Staten Island (background) and Brooklyn (foreground) in New York City. (Public domain image from Wikimedia Commons.)

So, this prompts the question: Do structural engineers really take into account the curvature of the Earth when designing and building large structures? The answer is—of course—yes, otherwise the large structures they build would be flawed.

There is a basic correction listed in The Engineering Handbook (published by CRC) to account for the curvature of the Earth. Section 162.5 says:

The curved shape of the Earth… makes actual level rod readings too large by the following approximate relationship: C = 0.0239 D2 where C is the error in the rod reading in feet and D is the sighting distance in thousands of feet.[4]

To convert to metric we need to multiply the constant by the number of feet in a metre (because of the squared factor), giving the correction in metres = 0.0784×(distance in km)2. What this means is that over a distance of 1 kilometre, the Earth’s surface curves downwards from a perfectly straight line by 78.4 millimetres. This correction is well known among civil and structural engineers, and is applied in surveying, railway line construction, bridge construction, and other areas. It means that for engineering purposes you can’t treat the Earth as both flat and level over distances of around a kilometre or more, because it isn’t. If you treat it as flat, then a kilometre away your level will be off by 78.4 mm. If you make a surface level (as measured by a level or inclinometer at each point) over a kilometre, then the surface won’t be flat; it will be curved parallel to the curvature of the Earth, and 78.4 mm lower than flat at the far end.

An example of this can be found at the Volkswagen Group test track facility near Ehra-Lessien, Germany. This track has a circuit of 96 km of private road, including a precision level-graded straight 9 km long. Over the 9 km length, the curvature of the Earth drops away from flat by 0.0784×92 = 6.35 metres. This means that if you stand at one end of the straight and someone else stands at the other end, you won’t be able to see each other because of the bulge of the Earth’s curvature in between. The effect can be seen in this video[5].

One set of structures where this difference was absolutely crucial is the Laser Interferometer Gravitational-Wave Observatory (LIGO) constructed at two sites in Hanford, Washington, and Livingston, Louisiana, in the USA.

LIGO site at Hanford

The LIGO site at Hanford, Washington. Each of the two arms of the structure are 4 km long. (Public domain image from Wikimedia Commons.)

LIGO uses lasers to detect tiny changes in length caused by gravitational waves from cosmic sources passing through the Earth. The lasers travel in sealed tubes 4 km long, which are under high vacuum. Because light travels in a straight line in a vacuum, the tubes must be absolutely straight for the machine to work. The tubes are level in the middle, but over the 2 km on either side, the curvature of the Earth falls away from a straight line by 0.0784×22 = 0.314 metres. So either end of the straight tube is 314 mm higher than the centre of the tube. To build LIGO, they laid a concrete foundation, but they couldn’t make it level over the distance; they had to make it straight. This required special construction techniques, because under normal circumstances (such as Volkswagen’s track at Ehra-Lessien) you want to build things level, not straight.[6]

So, the towers of large suspensions bridges almost certainly are not parallel, due to the curvature of the Earth, although it seems nobody has ever bothered to measure this. But it’s certainly true that structural engineers do take into account the curvature of the Earth for large building projects. They have to, because if they didn’t there would be significant errors and their constructions wouldn’t work as planned. If the Earth were flat they wouldn’t need to do this and wouldn’t bother.

UPDATE 2019-07-10: NASA’s Jet Propulsion Laboratory has announced a new technique which they can use to detect millimetre-sized shifts in the position of structures such as bridges, using aperture synthesis radar measurements from satellites. So maybe soon we can have more and better measurements of the positions of bridge towers![7]

References:

[1] Ashkenazi, V., Roberts, G. W. “Experimental monitoring of the Humber bridge using GPS”. Proceedings of the Institution of Civil Engineers – Civil Engineering, 120, p. 177-182, 1997. https://doi.org/10.1680/icien.1997.29810

[2] Roberts, G. W., Brown, C. J., Tang, X., Meng, X., Ogundipe, O. “A Tale of Five Bridges; the use of GNSS for Monitoring the Deflections of Bridges”. Journal of Applied Geodesy, 8, p. 241-264, 2014. https://doi.org/10.1515/jag-2014-0013

[3] Wikipedia: “Verrazzano-Narrows Bridge”, https://en.wikipedia.org/wiki/Verrazzano-Narrows_Bridge, accessed 2019-06-30. In turn, this page cites the following sources for the statement that the curvature of the Earth had to be taken into account during construction:

[3a] Rastorfer, D. Six Bridges: The Legacy of Othmar H. Ammann. Yale University Press, 2000, p. 138. ISBN 978-0-300-08047-6.

[3b] Caro, R.A. The Power Broker: Robert Moses and the Fall of New York. Knopf, 1974, p. 752. ISBN 978-0-394-48076-3.

[3c] Adler, H. “The History of the Verrazano-Narrows Bridge, 50 Years After Its Construction”. Smithsonian Magazine, Smithsonian Institution, November 2014.

[3d] “Verrazano-Narrows Bridge”. MTA Bridges & Tunnels. https://new.mta.info/bridges-and-tunnels/about/verrazzano-narrows-bridge, accessed 2019-06-30.

[4] Dorf, R. C. (editor). The Engineering Handbook, Second Edition, CRC Press, 2018, ISBN 978-0-849-31586-2.

[5] “Bugatti Veyron Top Speed Test”. Top Gear, BBC, 2008. https://youtu.be/LO0PgyPWE3o?t=200, accessed 2019-06-30.

[6] “Facts about LIGO”, LIGO Caltech web site. https://www.ligo.caltech.edu/page/facts, accessed 2019-06-30.

[7] “New Method Can Spot Failing Infrastructure from Space”, NASA JPL web site. https://www.jpl.nasa.gov/news/news.php?feature=7447, accessed 2019-07-10.

15. Trilateration

Trilateration is the method of locating points in space based on measuring the distances from known reference locations. It is used in surveying and navigation, similarly to the related method of triangulation, which technically uses the measurement of angles, not distances. For this entry we’re going to get practical and attempt to do some trilateration, using distances between some major cities in the world. To do this, I’ll need some equipment:

Equipment used

I acquired graph paper, a ruler, a tape measure, a pen, a pair of compasses, and a couple of large polystyrene balls.

I began my first scale drawing on a piece of graph paper. I’ve picked Auckland, New Zealand, as one of my cities of interest. Since nothing is on the paper yet, I can place Auckland wherever I want to. So I draw a cross indicating the position of Auckland and label it AKL (the city’s international airport code).

Auckland's position

For my second city, I’ve chosen Tokyo, Japan. According to a flight distance reference website, the travelling distance between Auckland and Tokyo, or more specifically between Auckland Airport and Tokyo’s Narita Airport, is 8806 kilometres. My graph paper has 2 mm squares, and (for reasons that will become clear in a minute) I’m using a scale of 86.1 km/mm. So I take a pair of compasses and set the distance from the metal point to the pen tip to be 102.3 mm as best I can. That’s 51 and a bit grid squares. I place the point in the centre of the AKL cross and mark a point on the paper 102.3 mm away with the pen tip. I enlarge the point to a cross and label it NRT (for Narita Airport). It doesn’t matter which direction I choose to place Tokyo from Auckland, because at this point there are no other constraints.

Tokyo's position

For my third city, I choose Los Angeles, USA. Los Angeles Airport, LAX, is 10467 km from Auckland, and 8773 km from Tokyo Narita. To locate LAX on my scale drawing, I first set my compasses with a distance of 10467 / 86.1 = 121.6 mm. With this distance setting, I draw an arc centred on AKL.

Los Angeles' position from Auckland

All of the points on this arc are the correct distance from Auckland to be Los Angeles. But we have another constraint – Los Angeles also has to be the correct distance from Tokyo. So I set my compasses to 8773 / 86.1 = 101.9 mm, and draw an arc centred at NRT.

Los Angeles' position nailed down

The intersection of these two arcs is the point that is both the correct scale distance from Auckland and Tokyo, so I label the intersection point LAX. So far, so good. We have three world cities with their relative positions accurately plotted to scale. Let’s add a fourth city! For the fourth city, I’ll choose something somewhere in the middle of the first three: Honolulu, USA. For starters, Honolulu is 7063 km from Auckland. So I draw an arc with radius 7063 / 86.1 = 82.0 mm centred on AKL.

Honolulu's position from Auckland

Honolulu is 6146 km from Tokyo. So I draw an arc with radius 6146 / 86.1 = 71.4 mm centred on NRT.

Honolulu's position from Auckland and Tokyo

Now in theory this is enough to give us the location of Honululu. It must be on both the arc centred at Auckland and on the arc centred at Tokyo – so it has to be at the intersection of those two arcs. But wait! We have more information than that. We also know that Honolulu is 4113 km from Los Angeles. So I draw an arc with radius 4113 / 86.1 = 47.8 mm centred on LAX.

Honolulu's position from Auckland, Tokyo, and Los Angeles

For the flight distances to be correct, Honolulu Airport (HNL) must be on all three arcs that I’ve drawn. But the arcs don’t all intersect at the same point. So where is Honolulu? According to the rules of geometry, anywhere we put it results in at least one of the distances being wrong. In the worst case, the the AKL-LAX intersection is 10 mm on the drawing from the NRT-LAX intersection, an error of 861 kilometres, which is 300 km longer than the entire chain of populated Hawaiian Islands from Niihau to Hawaii. Obviously a navigation error this large when trying to find Honolulu in the midst of the Pacific Ocean would be disastrous.

What’s gone wrong? Well, I’ve attempted to draw these distances to scale on a flat piece of paper. The error shows the distortion caused by trying to map the shape of the Earth onto a flat surface. The distances are all correct, but in reality they don’t lie in the same plane. So let’s try another approach. I’m going to map the distances onto a scale model of the Earth as a sphere.

To do this, I got a polystyrene sphere from an art supply shop. I measured the circumference using a tape measure to be 465 mm. Dividing the average circumference of the Earth by this gives me a scale of 86.1 km/mm (which is where I got the scale that I used for the drawing above). Now I just need to repeat the steps above, but plot the points and arcs on the surface of the sphere. But there’s one small wrinkle: flight distances are measured along the surface of the Earth, but the compasses step off the distance in a straight line, as measured through the Earth. To get the correct scale distance to set the compasses, we need to do a little geometry:

Geometry figure: surface distance versus straight line distance

The distance along the surface of the Earth is d, the distance through the Earth is x, and the radius of the Earth is r. In radians, the angle θ is d/r. Now according to the cosine rule of trigonometry:

x2 = r2 + r2 – 2r2 cos θ

x2 = 2r2(1 – cos(d/r))

So plugging in d and r we can find the distance x to set the compasses to (at the correct scale). Here’s a summary table:

Cities Distance (km) Scale distance (mm) Compasses distance (mm)
AKL-NRT 8806 102.3 94.3
AKL-LAX 10467 121.6 108.4
NRT-LAX 8773 102.0 94.0
AKL-HNL 7063 82.1 77.9
NRT-HNL 6146 71.4 68.6
LAX-HNL 4113 47.8 46.9

Using the distances in the Compasses column on my polystyrene sphere, and following the same steps as above for the graph paper, produced this:

Honolulu's position on a sphere

The arcs drawn with the correct scale distances of Honolulu from Auckland, Tokyo, and Los Angeles all intersect at exactly the same point on the surface of the sphere. We’ve found Honolulu!

So by experiment, trilateration of points on the Earth’s surface does not work if you use a flat surface to map the points. It only works if you use a sphere.

Addendum: I bought two spheres because I was prepared for the first attempt to be a little bit out due to any small inaccuracies or mistakes in my setting the correct compasses distances. But as it turned out I only needed the one. I was pleasantly surprised when it worked so well the first time.